Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Question 1

Câu 1:

Cho hàm số \(y = f(x)\) xác định và liên tục trên \(\mathbb{R}\)có bảng biến thiên như sau Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8 Số điểm cực tiểu của hàm số đã cho là:

A
1. \(0\)
B
2. \(3\)
C
3. \(1\)
D
4. \(2\)

Answer

1. \(\left( { - 3;2; - 1} \right).\)

Answer

1. \(\frac{{32\pi }}{3}\).

Answer

1. \( - 3\).

Answer

3. \(7!\).

Answer

1. \(( - 3;0)\).

Answer

4. \(y = - 3\).

Answer

3. \(C_5^2 + C_8^2\).

Answer

3. \(\overrightarrow k = \left( {0;0;1} \right)\).

Answer

3. \(x = 4\).

Answer

2. \(24\pi {a^2}\).

Answer

1. \(\int\limits_b^a {f\left( x \right)dx} = - \int\limits_a^b {f\left( x \right)} dx\).

Answer

2. \(\mathbb{R}\backslash \left\{ 1 \right\}\).

Answer

3. \(R = 3\).

Answer

1. \(y = - {x^4} + 3{x^2} - 1\).

Answer

4. \(\frac{{{x^4}}}{4} + 2{x^3} - 2x + C\).

Answer

1. \({S_{xq}} = 2\pi h\).

Answer

4. \(4{a^3}\).

Answer

3. \(P = 9\).

Answer

4. \(\cos x - x\sin x + C\).

Answer

3. \(x + z - 3 = 0\).

Answer

1. \(2x - y - z - 5 = 0\).

Answer

1. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\).

Answer

4. \(\frac{3}{{11}}\).

Answer

1. \(a > 0,b < 0,c < 0\).

Answer

2. \({u_3} = 4\)

Answer

3. \(\sqrt 3 {a^2}.\)

Answer

1. \(T = - 1.\)

Answer

1. \(2021.\)

Answer

3. \(a \in \left( {16;\left. {18} \right]} \right.\).

Answer

1. \(\frac{{a\sqrt {15} }}{5}\).

Answer

1. \(x - y - z = 0.\)

Answer

4. \(\frac{9}{2}\).

Answer

4. \(\frac{9}{4}\)

Answer

1. \(m = \pm 1\)

Answer

2. \({30^o}\)

Answer

2. \(7{a^3}\)

Answer

2. \(\left( { - 1;\frac{1}{2}} \right)\)

Answer

4. \(25\).

Answer

4. Vô số.

Answer

3. \(I = - \frac{{16}}{3}\).

Answer

1. \(2022\).

Question 2

Câu 2:

Trong không gian \(Oxyz\), tọa độ của véc tơ \(\overrightarrow a = 2\overrightarrow j – \mathop i\limits^ \to – 3\overrightarrow k \) là:

A
1. \(\left( { - 3;2; - 1} \right).\)
B
2. \(\left( {2; - 3; - 1} \right).\)
C
3. \(\left( {2; - 1; - 3} \right).\)
D
4. \(\left( { - 1;2; - 3} \right).\)

Question 3

Câu 3:

Cho khối cầu có bán kính \(r = 2\). Thể tích của khối cầu đã cho bằng

A
1. \(\frac{{32\pi }}{3}\).
B
2. \(\frac{{256\pi }}{3}\).
C
3. \(64\pi \).
D
4. \(256\pi \)

Question 4

Câu 4:

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên. Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8 Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { – 3\,;3} \right]\) bằng

A
1. \(0\)
B
2. \(8\)
C
3. \(1\)
D
4. \(3\)

Question 5

Câu 5:

Cho \(a > 0,a \ne 1\), biểu thức \(D = {\log _{{a^3}}}a\) có giá trị bằng bao nhiêu?

A
1. \( - 3\).
B
2. \( - \frac{1}{3}\).
C
3. \(3\).
D
4. \(\frac{1}{3}\).

Question 6

Câu 6:

Có bao nhiêu cách xếp 7 học sinh thành một hàng dọc?

A
1. \(7\).
B
2. \(1\).
C
3. \(7!\).
D
4. \(49\).

Question 7

Câu 7:

Cho hàm số có bảng biến thiên như sau: Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8 Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A
1. \(( - 3;0)\).
B
2. \(( - 5;2)\).
C
3. \(( - 5; + \infty )\).
D
4. \((2;4)\).

Question 8

Câu 8:

Tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x – 2}}{{4 – x}}\) là:

A
1. \(y = 2\).
B
2. \(x = - 3\).
C
3. \(y = \frac{3}{4}\).
D
4. \(y = - 3\).

Question 9

Câu 9:

Từ một nhóm gồm \(5\) học sinh nam và \(8\) học sinh nữ có bao nhiêu cách chọn ra hai học sinh bất kỳ?

A
1. \(C_{13}^2\).
B
2. \(13\).
C
3. \(C_5^2 + C_8^2\).
D
4. \(\mathop A\nolimits_{13}^3 \) .

Question 10

Câu 10:

Trong không gian \(Oxyz\), một vectơ pháp tuyến của mặt phẳng \(\left( {Oyz} \right)\) là

A
1. \(\overrightarrow i = \left( {1;0;0} \right)\).
B
2. \(\overrightarrow j = \left( {0;1;0} \right)\).
C
3. \(\overrightarrow k = \left( {0;0;1} \right)\).
D
4. \(\overrightarrow n = \left( {0;1;1} \right)\).

Question 11

Câu 11:

Phương trình \({\log _5}(2x – 3) = 1\)có nghiệm là

A
1. \(x = 2\).
B
2. \(x = 3\).
C
3. \(x = 4\).
D
4. \(x = 5\).

Question 12

Câu 12:

Cho hình nón có bán kính đáy bằng \(4a\) và chiều cao bằng \(3a\). Diện tích xung quanh của hình nón bằng

A
1. \(40\pi {a^2}\).
B
2. \(24\pi {a^2}\).
C
3. \(20\pi {a^2}\).
D
4. \(12\pi {a^2}\).

Question 13

Câu 13:

Cho hàm số \(f\left( x \right)\)liên tục trên đoạn \(\left[ {a;b} \right]\). Khẳng định nào sau đây sai?

A
1. \(\int\limits_b^a {f\left( x \right)dx} = - \int\limits_a^b {f\left( x \right)} dx\).
B
2. \(\int\limits_a^b {\left[ {f\left( x \right).g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} .\int\limits_a^b {g\left( x \right)dx} \).
C
3. \(\int\limits_a^b {k.f\left( x \right)dx} = k\int\limits_a^b {f\left( x \right)dx} ,k \in \mathbb{R}\).
D
4. \(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} \).

Question 14

Câu 14:

Hàm số \(y = {\left( {x – 1} \right)^{ – 4}}\) có tập xác định là

A
1. \(\left( {1; + \infty } \right)\).
B
2. \(\mathbb{R}\backslash \left\{ 1 \right\}\).
C
3. \(\mathbb{R}\).
D
4. \(\left( { - \infty ;1} \right)\).

Question 15

Câu 15:

Trong không gian \(Oxyz\), mặt cầu \((S):{(x – 5)^2} + {(y – 1)^2} + {(z + 2)^2} = 9\) có bán kính \(R\) là

A
1. \(R = 9\).
B
2. \(R = 18\).
C
3. \(R = 3\).
D
4. \(R = 6\).

Question 16

Câu 16:

Cho các hàm số \(y = f\left( x \right),y = g\left( x \right)\) liên tục trên \(\mathbb{R}\) có \(\int\limits_{ – 1}^5 {f\left( x \right){\text{dx}}} = – 1\); \(\int\limits_{ – 1}^5 {g\left( x \right){\text{dx}}} = 3\). Tính \(\int\limits_{ – 1}^5 {\left[ {f\left( x \right) + 2g\left( x \right)} \right]dx} \)

A
1. \(5\).
B
2. \(1\).
C
3. \( - 1\).
D
4. \(2\).

Question 17

Câu 17:

Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

A
1. \(y = - {x^4} + 3{x^2} - 1\).
B
2. \(y = {x^4} - 3{x^2} - 1\).
C
3. \(y = {x^3} - 3{x^2} - 1\).
D
4. \(y = - {x^3} + 3{x^2} - 1\).

Question 18

Câu 18:

Họ các nguyên hàm của hàm số \(f\left( x \right) = 5{x^4} – 6{x^2} + 1\) là

A
1. \(20{x^5} - 12{x^3} + x + C\).
B
2. \(20{x^3} - 12x + C\).
C
3. \({x^5} - 2{x^3} + x + C\).
D
4. \(\frac{{{x^4}}}{4} + 2{x^3} - 2x + C\).

Question 19

Câu 19:

Công thức tính diện tích xung quanh của hình trụ có đường cao \(h\), bán kính đường tròn đáy\(R\).

A
1. \({S_{xq}} = 2\pi h\).
B
2. \({S_{xq}} = 2Rh\).
C
3. \({S_{xq}} = {\pi ^2}Rh\).
D
4. \({S_{xq}} = 2\pi Rh\).

Question 20

Câu 20:

Cho hình chóp có đáy là hình vuông cạnh \(a\) và chiều cao bằng \(4a\). Thể tích khối chóp đã cho bằng

A
1. \(16{a^3}\).
B
2. \(\frac{4}{3}{a^3}\).
C
3. \(\frac{{13}}{3}{a^3}\).
D
4. \(4{a^3}\).

Question 21

Câu 21:

Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0;9} \right]\) thỏa mãn \(\int\limits_0^9 {f\left( x \right)} dx = 8,\,\,\int\limits_4^7 {f\left( x \right)} dx = 3.\) Khi đó giá trị của \(P = \int\limits_0^4 {f\left( x \right)} dx + \,\int\limits_7^9 {f\left( x \right)} dx\) là

A
1. \(P = 5\).
B
2. \(P = 11\).
C
3. \(P = 9\).
D
4. \(P = 20\).

Question 22

Câu 22:

Cho hàm số bậc bốn \(f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị trong hình bên.

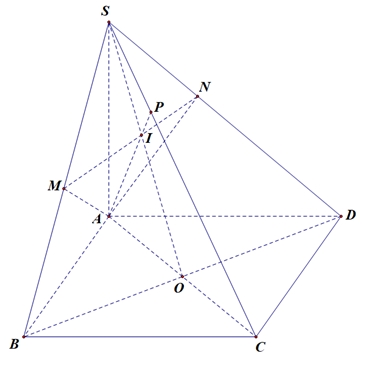
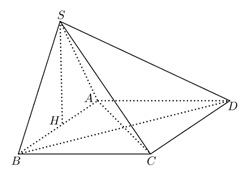
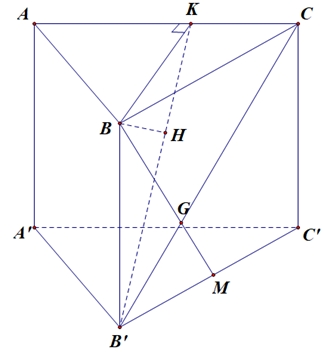
Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Số điểm cực đại của hàm số đã cho là

A
1. \(2\).
B
2. \(4\).
C
3. \(3\).
D
4. \(1\).

Question 23

Câu 23:

Họ nguyên hàm \(\int {x\cos x{\text{d}}x} \) là

A
1. \(\cos x + x\sin x + C\).
B
2. \( - \cos x + x\sin x + C\).
C
3. \( - \cos x - x\sin x + C\).
D
4. \(\cos x - x\sin x + C\).

Question 24

Câu 24:

Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right)\) đi qua điểm \(M\left( {2; – 5;1} \right)\) và song song với mặt phẳng \(\left( {Oxz} \right)\) có phương trình là:

A
1. \(x + y + 3 = 0\).
B
2. \(x - 2 = 0\).
C
3. \(x + z - 3 = 0\).
D
4. \(y + 5 = 0\).

Question 25

Câu 25:

Số nghiệm của phương trình \({\log _2}\left( {{x^2} – 6} \right) = {\log _2}\left( {x – 2} \right) + 1\) là:

A
1. \(0\)
B
2. \(1\).
C
3. \(3 \cdot \)
D
4. \(2\).

Question 26

Câu 26:

Trong không gian \(Oxyz\), cho hai điểm\(A\left( {1;3;0} \right)\)và\(B\left( {5;1; – 2} \right)\). Mặt phẳng trung trực của đoạn thẳng\(AB\)có phương trình là

A
1. \(2x - y - z - 5 = 0\).
B
2. \(3x + 2y - z - 14 = 0\).
C
3. \(2x - y - z + 5 = 0\).
D
4. \(x + 2y + 2z - 3 = 0\).

Question 27

Câu 27:

Trong không gian\(Oxyz\),phương trình mặt cầu\(\left( S \right)\)có tâm\(I\left( { – 1;2;1} \right)\)và đi qua điểm\(A\left( {0;4; – 1} \right)\)là

A
1. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\).
B
2. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 3\).
C
3. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 3\).
D
4. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9\).

Question 28

Câu 28:

Một bình đựng \(5\) quả cầu xanh khác nhau, \(4\) quả cầu đỏ khác nhau và \(3\) quả cầu vàng khác nhau. Chọn ngẫu nhiên \(3\) quả cầu trong quả cầu trên. Xác suất để chọn được \(3\) quả cầu khác màu là

A
1. \(\frac{3}{{14}}\).
B
2. \(\frac{3}{7}\).
C
3. \(\frac{3}{5}\).
D
4. \(\frac{3}{{11}}\).

Question 29

Câu 29:

Cho hàm số \(y = a{x^4} + b{x^2} + c{\text{ }}\left( {a \ne 0} \right)\) có đồ thị như hình bên.

Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Xác định dấu của \(a\,,\,b\,,\,c\).

A
1. \(a > 0,b < 0,c < 0\).
B
2. \(a > 0,b < 0,c > 0\).
C
3. \(a < 0,b < 0,c < 0\).
D
4. \(a > 0,b > 0,c < 0\).

Question 30

Câu 30:

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \frac{{x + 1}}{{{x^2} – 1}}\) là

A
1. 4
B
2. 2
C
3. 1
D
4. 3

Question 31

Câu 31:

Tập nghiệm của bất phương trình \(\log _2^2x – 5{\log _2}x + 6 \leqslant 0\) là \(S = \left[ {a;b} \right]\). Tính \(2a + b\).

A
1. \( - 8\)
B
2. \(8\)
C
3. \({\text{16}}\)
D
4. \(7\)

Question 32

Câu 32:

Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = 1\); công sai \(d = 2\). Số hạng thứ 3 của cấp số cộng đã cho là

A
1. \({u_3} = 3\)
B
2. \({u_3} = 4\)
C
3. \({u_3} = 7\)
D
4. \({u_3} = 5\)

Question 33

Câu 33:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm là \(f'\left( x \right) = {x^2}{\left( {2x – 1} \right)^2}\left( {x + 1} \right),\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là

A
1. \(1\)
B
2. \(3\)
C
3. \(0\)
D
4. \(2\)

Question 34

Câu 34:

Khối chóp tam giác có thể tích là: \(\frac{{2{a^3}}}{3}\) và chiều cao \(a\sqrt 3 \). Tìm diện tích đáy của khối chóp tam giác đó.

A
1. \(\frac{{2\sqrt 3 {a^2}}}{3}.\)
B
2. \(\frac{{2\sqrt 3 {a^2}}}{9}.\)
C
3. \(\sqrt 3 {a^2}.\)
D
4. \(2\sqrt 3 {a^2}.\)

Question 35

Câu 35:

Cho số thực \(x\) thoả mãn: \({25^x} – {5^{1 + x}} – 6 = 0\). Tính giá trị của biểu thức \(T = 5 – {5^x}\).

A
1. \(T = - 1.\)
B
2. \(T = \frac{5}{6}.\)
C
3. \(T = \frac{5}{6}.\)
D
4. \(T = \frac{5}{6}.\)

Question 36

Câu 36:

Cho hàm số \(f(x)\) là hàm đa thức bậc 3 và có đồ thị như hình vẽ. Xét hàm số \(g\left( x \right) = f\left( {2{x^3} + x – 1} \right) + m\). Với giá trị nào của m thì giá trị nhỏ nhất của \(g(x)\)trên đoạn \(\left[ {0;1} \right]\)bằng \(2022\). Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

A
1. \(2021.\)
B
2. \(2000.\)
C
3. \(2023.\)
D
4. \(2022.\)

Question 37

Câu 37:

Cho \(a\) là số thực dương sao cho \({3^x} + {a^x} \geqslant {6^x} + {9^x}\) với mọi \(x \in \mathbb{R}\). Mệnh đề nào sau đây đúng?

A
1. \(a \in \left( {12;\left. {14} \right]} \right.\).
B
2. \(a \in \left( {14;\left. {16} \right]} \right.\).
C
3. \(a \in \left( {16;\left. {18} \right]} \right.\).
D
4. \(a \in \left( {10;\left. {12} \right]} \right.\).

Question 38

Câu 38:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh bằng \(a\), \(\widehat {BAD} = {120^0}\). Mặt bên \(SAB\) là tam giác đều và \(\left( {SAB} \right) \bot \left( {ABCD} \right)\) (tham khảo hình vẽ).

Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Tính khoảng cách từ \(A\) đến \(\left( {SBC} \right)\)

A
1. \(\frac{{a\sqrt {15} }}{5}\).
B
2. \(\frac{{a\sqrt 7 }}{7}\).
C
3. \(\frac{a}{2}\).
D
4. \(\frac{{\sqrt 3 a}}{4}\).

Question 39

Câu 39:

Trong không gian \(Oxyz\), cho mặt cầu \({x^2} + {y^2} + {z^2} – 2x – 2y – 2z = 0\) và \(A\left( {2;2;\,0} \right)\). Viết phương trình mặt phẳng \(\left( {OAB} \right)\) biết \(B\) thuộc mặt cầu \(\left( S \right)\), có hoành độ dương và tam giác \(OAB\) đều.

A
1. \(x - y - z = 0.\)
B
2. \(x - y - 2z = 0\)
C
3. \(x - y + 2z = 0\)
D
4. \(x - y + z = 0\)

Question 40

Câu 40:

Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – \frac{1}{2}\)và \(g\left( x \right) = d{x^2} + ex + 1\) \((a,b,c,d,e \in \mathbb{R})\). Biết rằng đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại 3 điểm có hoành độ lần lượt là \( – 3\); \( – 1\); \(1\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

A
1. \(4\).
B
2. \(8\).
C
3. \(5\).
D
4. \(\frac{9}{2}\).

Question 41

Câu 41:

Cho hàm số \(f\left( x \right)\) có đồ thị hình vẽ

Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Phương trình \(f\left( {f\left( x \right)} \right) = 0\) có bao nhiêu nghiệm thực?

A
1. \(3\)
B
2. \(7\)
C
3. \(9\)
D
4. \(5\)

\(f\left( {f\left( x \right)} \right) = 0 \Leftrightarrow \left[ \begin{gathered} f\left( x \right) = {x_1},\,\,{x_1} \in \left( { – 2; – 1} \right) \hfill \\ f\left( x \right) = {x_2},\,\,{x_2} \in \left( {0;1} \right) \hfill \\ f\left( x \right) = {x_3},\,\,{x_3} \in \left( {1;2} \right) \hfill \\ \end{gathered} \right.\).Dựa vào đồ thị ta thấy:+) \(f\left( x \right) = {x_1},\,\,{x_1} \in \left( { – 2; – 1} \right)\) cho ta \(3\) nghiệm phân biệt.+) \(f\left( x \right) = {x_2},\,\,{x_2} \in \left( {0;1} \right)\) cho ta \(3\) nghiệm phân biệt.+) \(f\left( x \right) = {x_3},\,\,{x_3} \in \left( {1;2} \right)\) cho ta \(3\) nghiệm phân biệt.

Vậy phương trình đã cho có \(9\) nghiệm phân biệt.

Question 42

Câu 42:

Cho hàm số \(f\left( x \right)\) liên tục trên khoảng \(\left( {0; + \infty } \right)\) và thỏa mãn \(2f\left( x \right) + xf\left( {\frac{1}{x}} \right) = x\) với mọi \(x > 0\). Tính \(\int\limits_{\frac{1}{2}}^2 {f\left( x \right)dx.} \)

A
1. \(\frac{7}{4}\)
B
2. \(\frac{3}{4}\)
C
3. \(\frac{7}{{12}}\)
D
4. \(\frac{9}{4}\)

Xét \(2f\left( x \right) + xf\left( {\frac{1}{x}} \right) = x\) (1)Thay \(x = \frac{1}{x}\) ta có: \(\left( 1 \right) \Leftrightarrow 2f\left( {\frac{1}{x}} \right) + \frac{1}{x}.f\left( x \right) = \frac{1}{x}\)\( \Leftrightarrow x\left[ {2f\left( {\frac{1}{x}} \right) + \frac{1}{x}.f\left( x \right)} \right] = x.\frac{1}{x}\)\( \Leftrightarrow 2xf\left( {\frac{1}{x}} \right) + f\left( x \right) = 1\) (2)Mặt khác: \(\left( 1 \right) \Leftrightarrow 2\left[ {2f\left( x \right) + xf\left( {\frac{1}{x}} \right)} \right] = 2x\)\( \Leftrightarrow 4f\left( x \right) + 2xf\left( {\frac{1}{x}} \right) = 2x\) (3)Lấy (3) trừ (2) ta được: \(f\left( x \right) = \frac{1}{3}\left( {2x – 1} \right)\)Do đó: \(\int\limits_{\frac{1}{2}}^2 {f\left( x \right)dx} = \frac{1}{3}\int\limits_{\frac{1}{2}}^2 {\left( {2x – 1} \right)dx} = \left. {\frac{1}{3}\left( {{x^2} – x} \right)} \right|_{\frac{1}{2}}^2 = \frac{3}{4}\).

Question 43

Câu 43:

Trong không gian tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right)\) có phương trình là \({x^2} + {y^2} + {z^2} – 2x + 2my – 4z – 1 = 0\) (trong đó \(m\) là tham số). Tìm tất cả các giá trị của \(m\) để mặt cầu \(\left( S \right)\) có diện tích bằng \(28\pi \).

A
1. \(m = \pm 1\)
B
2. \(m = \pm 2\)
C
3. \(m = \pm 3\)
D
4. \(m = \pm 7\)

Ta có: \({x^2} + {y^2} + {z^2} – 2x + 2my – 4z – 1 = 0 \Leftrightarrow {\left( {x – 1} \right)^2} + {\left( {y + m} \right)^2} + {\left( {z – 2} \right)^2} = {m^2} + 6\).\(S = 28\pi \Leftrightarrow 4\pi {R^2} = 28\pi \Leftrightarrow {m^2} + 6 = 7 \Leftrightarrow m = \pm 1\).

Question 44

Câu 44:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\); \(SA = a\sqrt 2 \) và \(SA\) vuông góc với mặt đáy \(\left( {ABCD} \right)\). Gọi \(M\); \(N\) lần lượt là hình chiếu vuông góc của đỉnh \(A\) lên các cạnh \(SB\) và \(SD\). Khi đó góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {AMN} \right)\) bằng

A
1. \({45^o}\)
B
2. \({30^o}\)
C
3. \({90^o}\)
D
4. \({60^o}\)

Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Cách 1:Gọi \(AC \cap BD = O,\,\,SO \cap MN = I,\,\,AI \cap SC = P\).\(AN \bot \left( {SCD} \right) \Rightarrow AN \bot SC\) và \(AM \bot \left( {SBC} \right) \Rightarrow AM \bot SC\), do đó: \(SC \bot \left( {AMN} \right)\) hay \(SC \bot \left( {AMPN} \right)\).Suy ra: \(\left( {SB,\left( {AMN} \right)} \right) = \left( {SM,\left( {AMPN} \right)} \right) = \widehat {SMP}\).Ta có: \(SM = \frac{{S{A^2}}}{{SB}} = \frac{{2{a^2}}}{{\sqrt {2{a^2} + {a^2}} }} = \frac{{2a\sqrt 3 }}{3}\); \(SP = \frac{{S{A^2}}}{{SC}} = \frac{{2{a^2}}}{{\sqrt {2{a^2} + 2{a^2}} }} = a\).Nên \(\sin \widehat {SMP} = \frac{{SP}}{{SM}} = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat {SMP} = {60^o}\).

Cách 2:Ta có \(AM = AN = \frac{{a\sqrt 6 }}{3}\) và \(\frac{{SM}}{{SB}} = \frac{{SN}}{{SD}} = \frac{{S{A^2}}}{{S{B^2}}} = \frac{2}{3} \Rightarrow MN\parallel BD;\frac{{MN}}{{BD}} = \frac{2}{3}\)Suy ra \(MN = \frac{2}{3}BD = \frac{{2a\sqrt 2 }}{3}\)

Diện tích tam giác \(AMN:{S_{\Delta AMN}} = \frac{{2{a^2}\sqrt 2 }}{9}\)\({V_{S.AMN}} = \frac{2}{3}.\frac{2}{3}.{V_{S.ABD}} \Rightarrow {V_{S.AMN}} = \frac{1}{3}.\frac{4}{9}.\frac{1}{2}.a\sqrt 2 .{a^2} = \frac{{2\sqrt 2 .{a^3}}}{{27}}\)

\(\Rightarrow d\left( {S;\left( {AMN} \right)} \right) = \frac{{3{V_{S.AMN}}}}{{{S_{\Delta AMN}}}} = a\)

Do đó,

\(\sin \left( {\widehat {SB;(AMN)}} \right) = \frac{{d\left( {S;(AMN)} \right)}}{{SM}} = \frac{{\sqrt 3 }}{2}\)

\( \Rightarrow \left( {\widehat {SB;(AMN)}} \right) = {60^0}\)

Question 45

Câu 45:

Cho khối lăng trụ đứng \(ABC.A'B'C'\) có \(\widehat {BAC} = 60^\circ \), \(AB = 3a\) và \(AC = 4a\). Gọi \(M\) là trung điểm của \(B'C'\), biết khoảng các từ \(M\) đến mặt phẳng \(\left( {B'AC} \right)\) bằng \(\frac{{3a\sqrt {15} }}{{10}}\). Thể tích khối lăng trụ bằng

A
1. \(9{a^3}\)
B
2. \(7{a^3}\)
C
3. \(27{a^3}\)
D
4. \(4{a^3}\)

Gọi \(B'C \cap BM = G\), ta có: \(\frac{{d\left( {M;\left( {B'AC} \right)} \right)}}{{d\left( {B;\left( {B'AC} \right)} \right)}} = \frac{{MG}}{{BG}} = \frac{{B'M}}{{BC}} = \frac{1}{2} \Rightarrow d\left( {B;\left( {B'AC} \right)} \right) = \frac{{3a\sqrt {15} }}{5}\).

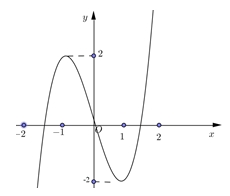
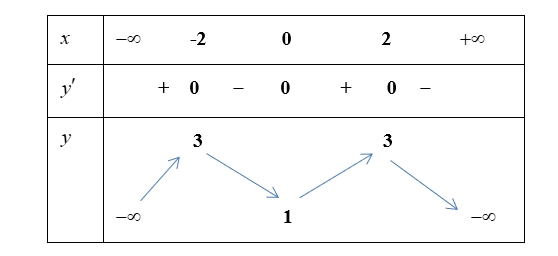Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Kẻ \(BK \bot AC\), mà \(AC \bot BB'\) nên \(AC \bot \left( {BB'K} \right) \Rightarrow \left( {B'AC} \right) \bot \left( {BB'K} \right)\).

\(\left( {B'AC} \right) \cap \left( {BB'K} \right) = B'K\), trong mp\(\left( {B'BK} \right)\) kẻ \(BH \bot B'K\), khi đó: \(BH \bot \left( {B'AC} \right)\).

Do đó: \(d\left( {B;\left( {B'AC} \right)} \right) = BH = \frac{{3a\sqrt {15} }}{5}\).

\(\Delta AKB\) vuông tại \(K\) nên \(BK = A

B:)\sin {60^o} = 3a.\frac{{\sqrt 3 }}{2} = \frac{{3a\sqrt 3 }}{2}\).

Mặt khác: \(\frac{1}{{B{H^2}}} = \frac{1}{{B{K^2}}} + \frac{1}{{B{{B'}^2}}} \Leftrightarrow \frac{1}{{{{\left( {\frac{{3a\sqrt {15} }}{5}} \right)}^2}}} = \frac{1}{{{{\left( {\frac{{3a\sqrt 3 }}{2}} \right)}^2}}} + \frac{1}{{B{{B'}^2}}} \Leftrightarrow BB' = 3a\sqrt 3 \).

Vậy \(V = BB'.{S_{\Delta ABC}} = 3a\sqrt 3 .\frac{1}{2}.3a.4a.\sin {60^o} = 27{a^3}\).

Question 46

Câu 46:

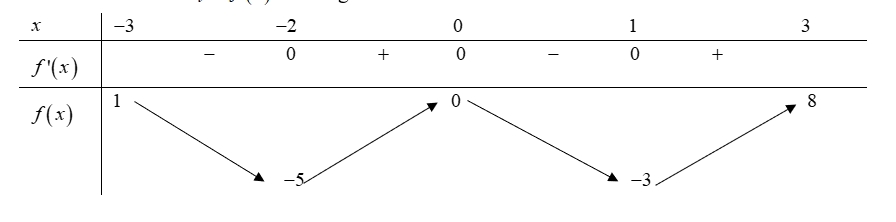Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trên \(\left[ { – 2;4} \right]\), gọi \({x_0}\) là điểm mà tại đó hàm số \(g\left( x \right) = f\left( {\frac{x}{2} + 1} \right) – \ln \left( {{x^2} + 8x + 16} \right)\) đạt giá trị lớn nhất. Khi đó \({x_0}\) thuộc khoảng nào? Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

A
1. \(\left( {\frac{1}{2};2} \right)\)
B
2. \(\left( { - 1;\frac{1}{2}} \right)\)
C
3. \(\left( {2;\frac{5}{2}} \right)\)
D
4. \(\left( { - 1; - \frac{1}{2}} \right)\)

Ta có: \(g'\left( x \right) = \frac{1}{2}f'\left( {\frac{x}{2} + 1} \right) – \frac{{2x + 8}}{{{x^2} + 8x + 16}} = \frac{1}{2}f'\left( {\frac{x}{2} + 1} \right) – \frac{2}{{x + 4}}\).\(g'\left( x \right) = 0 \Leftrightarrow f'\left( {\frac{x}{2} + 1} \right) = \frac{4}{{x + 4}}\) (1)Đặt \(t = \frac{x}{2} + 1\,\,,\,\,\left( {t \in \left[ {0;3} \right]} \right)\) ; khi đó: \(\left( 1 \right) \Leftrightarrow f'\left( t \right) = \frac{2}{{t + 1}}\).Ta có đồ thị biểu diễn sự tương giao của hai đồ thị là: 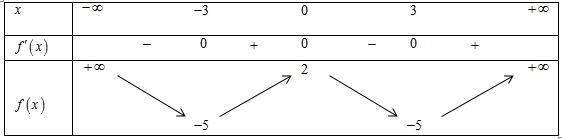Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

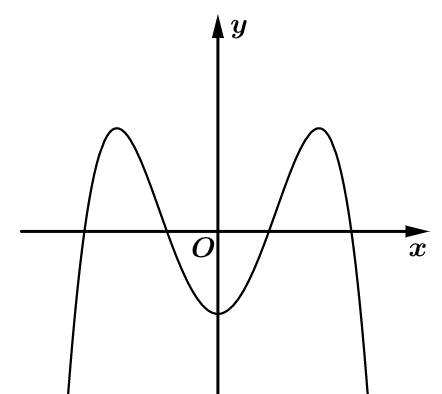
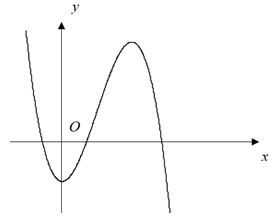
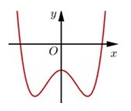
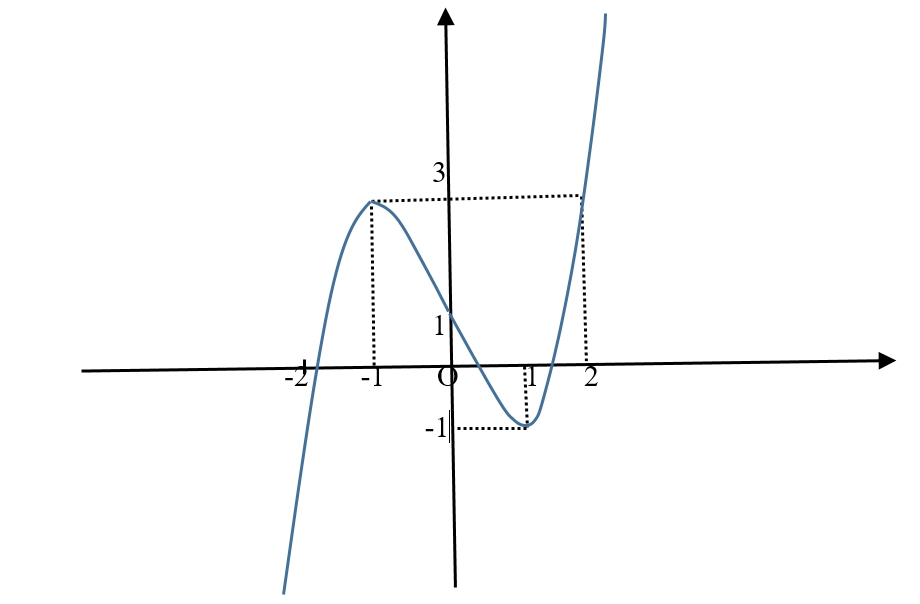
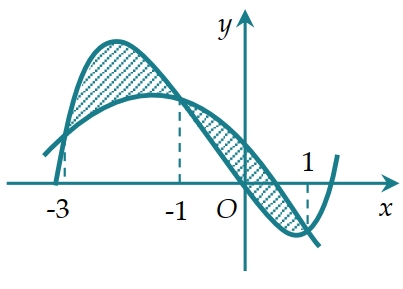
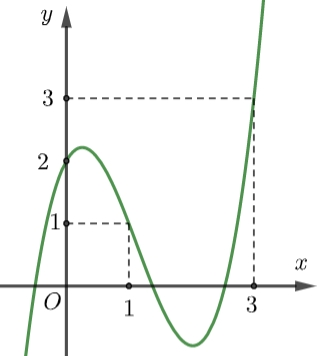
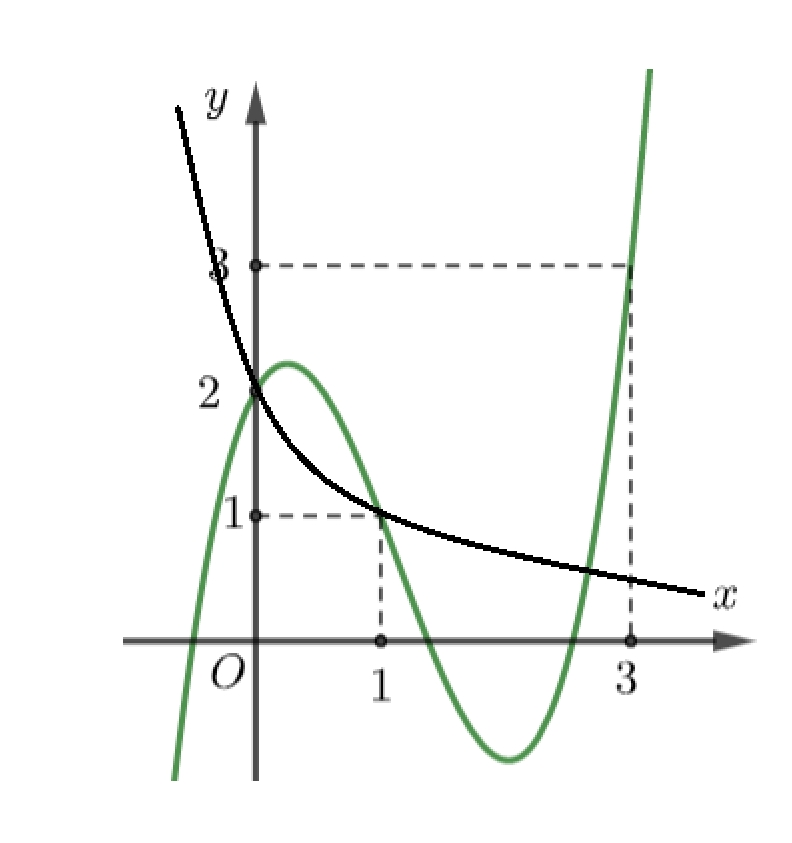Dựa vào đồ thị ta có GTLN của \(g\left( x \right)\) là tại \(g\left( 1 \right)\) hoặc \(g\left( 3 \right)\).Ta thấy: \(\int\limits_1^a {\left[ {\frac{2}{{t + 1}} – f'\left( t \right)} \right]dt} > \int\limits_a^3 {\left[ {f'\left( t \right) – \frac{2}{{t + 1}}} \right]dt} \)\( \Leftrightarrow \left. {\left( {2\ln \left| {t + 1} \right| – f\left( t \right)} \right)} \right|_1^a > \left. {\left( {f\left( t \right) – 2\ln \left| {t + 1} \right|} \right)} \right|_a^3\)\( \Leftrightarrow 2\ln \left( {a + 1} \right) – f\left( a \right) – 2\ln 2 + f\left( 1 \right) > f\left( 3 \right) – 4\ln 2 – f\left( a \right) + 2\ln \left( {a + 1} \right)\)\( \Leftrightarrow f\left( 1 \right) – f\left( 3 \right) + 2\ln 2 > 0\) (*)Xét \(g\left( x \right) = f\left( {\frac{x}{2} + 1} \right) – \ln \left( {{x^2} + 8x + 16} \right)\), khi đó:+) \(g\left( 1 \right) = f\left( 1 \right) – 4\ln 2\).+) \(g\left( 3 \right) = f\left( 3 \right) – 8\ln 2\).\( \Rightarrow g\left( 1 \right) – g\left( 3 \right) = f\left( 1 \right) – f\left( 3 \right) + 4\ln 2\), từ (*) ta suy ra \( \Rightarrow g\left( 1 \right) – g\left( 3 \right) > 0 \Leftrightarrow g\left( 1 \right) > g\left( 3 \right)\).Vậy hàm số đã cho đạt GTLN tại \(t = 1 \Rightarrow x = 0\).

Question 47

Câu 47:

Trong không gian cho hai điểm \(I\left( {2;3;3} \right)\)và \(J\left( {4; – 1;1} \right)\). Xét khối trụ \(\left( T \right)\) có hai đường tròn đáy nằm trên mặt cầu đường kính \(IJ\) và có hai tâm nằm trên đường thẳng \(IJ\). Khi có thể tích \(\left( T \right)\) lớn nhất thì hai mặt phẳng chứa hai đường tròn đáy của \(\left( T \right)\) có phương trình dạng \(x + by + cz + {d_1} = 0\) và \(x + by + cz + {d_2} = 0\). Giá trị của \(d_1^2 + d_2^2\) bằng:

A
1. \(61\).
B
2. \(14\).
C
3. \(26\).
D
4. \(25\).

Gọi mặt cầu \(\left( S \right)\) có đường kính \(IJ\) suy ra mặt cầu \(\left( S \right)\)có tâm \(K\) là trung điểm của \(IJ\) và bán kính \(R = \frac{{IJ}}{2}\)Ta có \(K\left( {3;1;2} \right),\,R = \sqrt 6 \)Xét khối trụ \(\left( T \right)\) có chiều cao \(2h\)thì bán kính \(R = \sqrt {6 – {h^2}} \)Khi đó thể tích khối trụ \(\left( T \right)\) là \(V = \pi {R^2}.2h = 2\pi .h.\left( {6 – {h^2}} \right)\,\,\,\,\left( {0 < h < \sqrt 6 } \right)\)Ta có \(V' = 12\pi - 6\pi {h^2};\,\,V' = 0 \Leftrightarrow h = \sqrt 2 \)Bảng biến thiênVậy \({V_{\max }} = 8\pi \sqrt 2 \,\,khi\,\,h = \sqrt 2 \)Ta có \(\overrightarrow {IJ} = \left( {2; – 4; – 2} \right) = 2\left( {1; – 2; – 1} \right)\)Suy ra phương trình 2 mặt phẳng lần lượt là \(\left( P \right):\,x – 2y – z + {d_1} = 0\) và \(\left( Q \right):\,x – 2y – z + {d_2} = 0\)Vì \(d\left( {K,\left( P \right)} \right) = h = \sqrt 2 \Rightarrow \frac{{\left| {3 – 2.1 – 2 + {d_1}} \right|}}{{\sqrt 6 }} = \sqrt 2 \Rightarrow \left[ \begin{gathered} {d_1} = 1 + 2\sqrt 3 \hfill \\ {d_1} = 1 – 2\sqrt 3 \hfill \\ \end{gathered} \right.\)Vì vai trò của \(\left( P \right),\,\left( Q \right)\)là như nhau nên \({d_1} = 1 + 2\sqrt 3 \Rightarrow {d_2} = 1 – 2\sqrt 3 \)Vậy \({d_1}^2 + {d_2}^2 = {\left( {1 – 2\sqrt 3 } \right)^2} + {\left( {1 + 2\sqrt 3 } \right)^2} = 26.\)

Question 48

Câu 48:

Trong hệ trục \(Oxyz\),cho hai mặt cầu \(({S_1}):{(x – 1)^2} + {(y + 3)^2} + {(z – 2)^2} = 49\)và \(({S_2}):{(x – 10)^2} + {(y – 9)^2} + {(z – 2)^2} = 400\)và mặt phẳng \((P):4x – 3y + mz + 22 = 0.\)Có bao nhiêu số nguyên m để mặt phẳng (P) cắt 2 mặt cầu \(\left( {{S_1}} \right)\),\(\left( {{S_2}} \right)\)theo giao tuyến là hai đường tròn không có tiếp tuyến chung?

A
1. \(11.\)
B
2. \(6.\)
C
3. \(5.\)
D
4. Vô số.

Mặt cầu \(\left( {{S_1}} \right)\) có tâm \({I_1}(1; – 3;2),{R_1} = 7;\) Mặt cầu \(\left( {{S_2}} \right)\) có tâm \({I_2}(10;9;2),{R_2} = 20;\)Ta có \({I_1}{I_2} = 15\),mà mặt phẳng (P) có vec tơ pháp tuyến \(\overrightarrow n = (4; – 3;m)\)Do \(\overrightarrow {{I_1}{I_2}} .\overrightarrow n = 0\) nên \({I_1}{I_2}\) song song hoặc nằm trong (P). Bán kính đường tròn giao tuyến của hai mặt cầu là \(\begin{gathered} S = \sqrt {p(p – 15)(p – 21)(p – 20)} = \frac{1}{2}15.R,p = 21 \hfill \\ \to R = 28/5 \hfill \\ \end{gathered} \) Phương trình mặt phẳng chứa đường tròn giao tuyến là :3x+4y+30=0 (Q) \(d({I_1};Q) = 21/5;d({I_2};Q) = 96/5 \Rightarrow ;d({I_1};Q) + {I_1}{I_2} = d({I_2};Q)\) Mặt phẳng (P) cắt 2 mặt cầu \(\left( {{S_1}} \right)\),\(\left( {{S_2}} \right)\)theo giao tuyến là hai đường tròn không có tiếp tuyến chung,trong đó đường tròn nhỏ ở trong đường tròn lớn khi \(\begin{gathered} 28/5 < d({I_1};(P)) < 7 \Leftrightarrow 28/5 < \frac{{\left| {2m + 35} \right|}}{{\sqrt {{m^2} + 25} }} < 7 \hfill \\ \Leftrightarrow \left\{ \begin{gathered} 45{m^2} - 140m > 0 \hfill \\ \frac{{684}}{{25}}{m^2} – 140m – 441 < 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \) Do m nguyên nên m là:-2;-1;4;5;6;7.Vậy có 6 giá trị m.

Question 49

Câu 49:

Cho hàm số \(f\left( x \right)\) nhận giá trị dương, có đạo hàm liên tục trên \(\left[ {0;2} \right]\). Biết \(f\left( 0 \right) = 1\) và \(f\left( x \right)f\left( {2 – x} \right) = {e^{2{x^2} – 4x}}\) với mọi \(x \in \left[ {0;2} \right]\). Tính tích phân \(I = \int\limits_0^2 {\frac{{\left( {{x^3} – 3{x^2}} \right)f'\left( x \right)}}{{f\left( x \right)}}dx} \)

A
1. \(I = - \frac{{14}}{3}\).
B
2. \(I = - \frac{{32}}{5}\).
C
3. \(I = - \frac{{16}}{3}\).
D
4. \(I = - \frac{{16}}{5}\).

Vì hàm số \(f\left( x \right)\) nhận giá trị dương, có đạo hàm liên tục trên \(\left[ {0;2} \right]\) và \(f\left( x \right)f\left( {2 – x} \right) = {e^{2{x^2} – 4x}}\) nên thay \(x = 0\), ta có: \(f\left( 0 \right).f\left( 2 \right) = 1\) mà \(f\left( 0 \right) = 1\) \( \Rightarrow f\left( 2 \right) = 1\).

Đặt:

\(\left\{ \begin{gathered}

u = {x^3} – 3{x^2} \hfill \\

{d}v = \frac{{f’\left( x \right)}}{{f\left( x \right)}}{d}x \hfill \\

\end{gathered} \right.\)\( \Rightarrow \left\{ \begin{gathered}

{d}u = \left( {3{x^2} – 6x} \right){d}x \hfill \\

v = \ln \left| {f\left( x \right)} \right| \hfill \\

\end{gathered} \right.\)\( \Rightarrow \left\{ \begin{gathered}

{d}u = \left( {3{x^2} – 6x} \right){d}x \hfill \\

v = \ln f\left( x \right) \hfill \\

\end{gathered} \right.\)

Suy ra: \(I = \left. {\left( {{x^3} – 3{x^2}} \right)\ln f\left( x \right)} \right|_0^2 – \int\limits_0^2 {\left( {3{x^2} – 6x} \right)\ln f\left( x \right){d}x} \)\( = – \int\limits_0^2 {\left( {3{x^2} – 6x} \right)\ln f\left( x \right){d}x} \) \(\left( 1 \right)\)

Đặt \(x = 2 – t\)\( \Rightarrow {d}x = – {d}t\).

Khi \(x = 0 \to t = 2\) và \(x = 2 \to t = 0\).

Khi đó, \(J = – \int\limits_2^0 {\left( {3{t^2} – 6t} \right)\ln f\left( {2 – t} \right)( – {d}t)} \)\( = – \int\limits_0^2 {\left( {3{t^2} – 6t} \right)\ln f\left( {2 – t} \right){d}t} \).

Vì tích phân không phụ thuộc vào biến nên \(I = – \int\limits_0^2 {\left( {3{x^2} – 6x} \right)\ln f\left( {2 – x} \right){d}x} \) \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), ta cộng vế theo vế, ta được: \(2I = – \int\limits_0^2 {\left( {3{x^2} – 6x} \right)\left[ {\ln f\left( x \right) + \ln f\left( {2 – x} \right)} \right]{d}x} \).

Hay \(I = – \frac{1}{2}\int\limits_0^2 {\left( {3{x^2} – 6x} \right)\left( {2{x^2} – 4x} \right){d}x} = – \frac{{16}}{5}\)

Question 50

Câu 50:

Cho phương trình \(\ln \left( {x + m} \right) – {e^x} + m = 0\), với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên \(m \in \left[ { – 2023;2023} \right]\) để phương trình đã cho có nghiệm?

A
1. \(2022\).
B
2. \(2021\).
C
3. \(4042\).
D
4. \(2023\).

Ta có: điều kiện: \(x + m > 0\)

\(\ln \left( {x + m} \right) = {e^x} – m = t \Leftrightarrow \left\{ \begin{gathered} x + m = {e^t} \hfill \\ t + m = {e^x} \hfill \\ \end{gathered} \right. \Leftrightarrow {e^t} + t = {e^x} + x\)

Xét hàm số: \(f(t) = {e^t} + t \Rightarrow {f^/}(t) = e{}^t + 1 > 0\,\,(\forall t \in \mathbb{R})\)

Nên ta có: \(f(t) = f(x) \Leftrightarrow t = x\)

Phương trình \({e^x} – m = x \Leftrightarrow {e^x} – x = m\) có nghiệm khi và chỉ khi \(m \geqslant 1\)

Vậy có: 2023 giá trị \(m\).

Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Đề Kiểm Tra: Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Các lựa chọn đã được chọn:

Đáp án: Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Trắc Nghiệm Liên Quan

Đề Ôn Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 7

Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Online Môn Toán-Đề 4

Trắc Nghiệm Online Bài Tập Hợp Lớp 10-Đề 9

Đề Luyện Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 9

Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

Đề Luyện Thi TN THPT 2023 Môn Toán Online-Đề 11

Đề Ôn Thi TN THPT 2023 Môn Toán Online-Đề 12

Đề Ôn Thi TN THPT Năm 2023 Môn Toán Online-Đề 13

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN