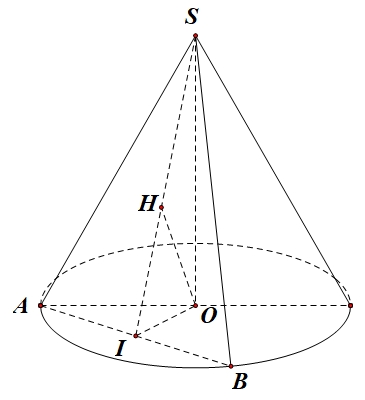
Xét hình nón đỉnh \(S\) có chiều cao \(h = SO = 2a\).Thiết diện đi qua đỉnh của hình nón là tam giác \(SAB\) cân tại \(S\).
+ Gọi \(I\) là trung điểm của đoạn thẳng \(AB\).
Trong tam giác \(SOI\), kẻ \(OH \bot SI\), \(H \in SI\).
+ \(\left\{ \begin{gathered} AB \bot OI \hfill \\ AB \bot SO \hfill \\ \end{gathered} \right. \Rightarrow AB \bot \left( {SOI} \right) \Rightarrow AB \bot OH\).
+\(\left\{ \begin{gathered} OH \bot SI \hfill \\ OH \bot AB \hfill \\ \end{gathered} \right.\)
\( \Rightarrow OH \bot \left( {SAB} \right)\)\( \Rightarrow d\left( {O\,,\,\left( {SAB} \right)} \right) = OH = \frac{{3a}}{2}\).
Xét tam giác \(SOI\)vuông tại \(O\), ta có \(\frac{1}{{O{I^2}}} = \frac{1}{{O{H^2}}} – \frac{1}{{S{O^2}}} = \frac{4}{{9{a^2}}} – \frac{1}{{4{a^2}}} = \frac{7}{{36{a^2}}}\) \( \Rightarrow OI = \frac{{6a}}{{\sqrt 7 }}\).và \(SI = \sqrt {O{I^2} + S{O^2}} = \sqrt {{{\left( {\frac{{6a}}{{\sqrt 7 }}} \right)}^2}+ {{\left( {2a} \right)}^2}} = \frac{{8a\sqrt 7 }}{7}\).
Ta có \({S_{\Delta SAB}} = \frac{{24{a^2}\sqrt 3 }}{7} \Leftrightarrow \frac{1}{2}SI.AB = \frac{{24{a^2}\sqrt 3 }}{7} \Rightarrow AB = \frac{{6a\sqrt {21} }}{7} \Rightarrow IA = \frac{{AB}}{2} = \frac{{3a\sqrt {21} }}{7}\)
Xét tam giác \(IAO\)vuông tại \(I \Rightarrow R = OA = \sqrt {O{I^2} + I{A^2}} = \sqrt {{{\left( {\frac{{6a}}{{\sqrt 7 }}} \right)}^2} + {{\left( {\frac{{3a\sqrt {21} }}{7}} \right)}^2}} = 3a\).
Thể tích của khối nón giới hạn bởi hình nón là: \(V = \frac{1}{3}h.\pi {R^2} = \frac{1}{3}.2a.\pi .{\left( {3a} \right)^2} = 6\pi {a^3}.\)

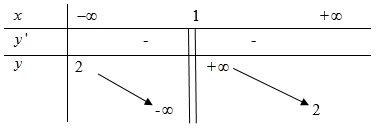 Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho lần lượt là
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho lần lượt là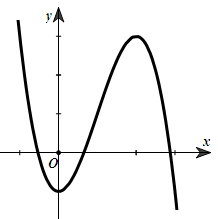
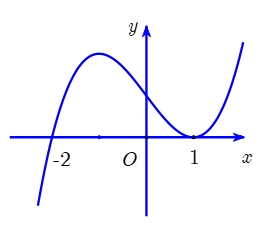

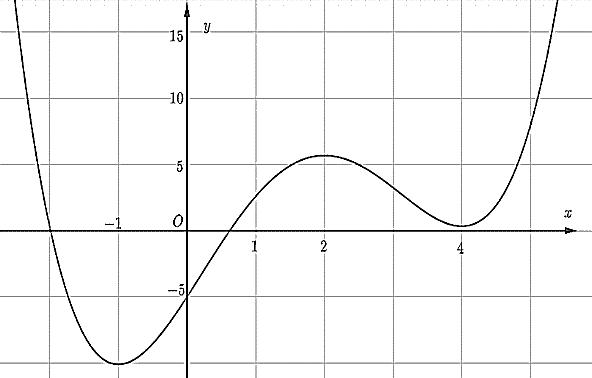 Số nghiệm thực phân biệt của phương trình \({\log _{\sqrt 2 }}(x – 1).f'(f(x)) = 0\) là
Số nghiệm thực phân biệt của phương trình \({\log _{\sqrt 2 }}(x – 1).f'(f(x)) = 0\) là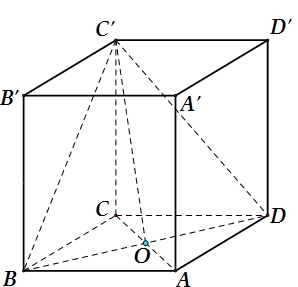

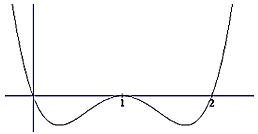 Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {{x^2} – 8x + m} \right)\) có \(5\) điểm cực trị
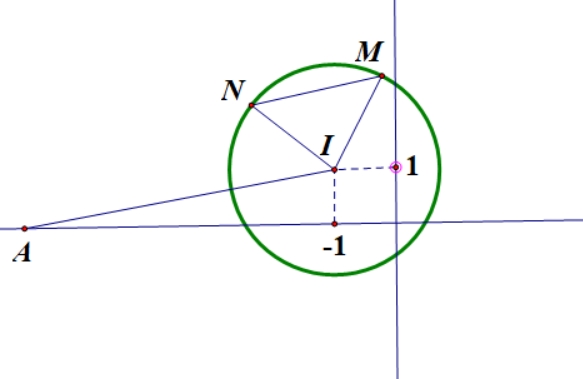
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {{x^2} – 8x + m} \right)\) có \(5\) điểm cực trị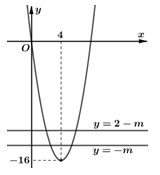 Khi đó \(\left( * \right){\text{ }} \Leftrightarrow {\text{ }}{d_1},{\text{ }}{d_2}\) cắt \(\left( C \right)\) tại bốn điểm phân biệt \( \Leftrightarrow – m > – 16 \Leftrightarrow m < 16.\)
Khi đó \(\left( * \right){\text{ }} \Leftrightarrow {\text{ }}{d_1},{\text{ }}{d_2}\) cắt \(\left( C \right)\) tại bốn điểm phân biệt \( \Leftrightarrow – m > – 16 \Leftrightarrow m < 16.\)