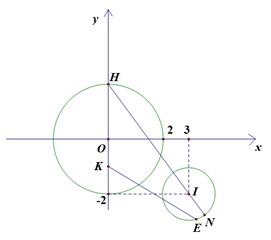
Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

Question 1

Câu 1:

Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2\), \({u_2} = 6\). Công sai của cấp số cộng bằng

A
1. 3.
B
2. 4.
C
3. \( - 4.\)
D
4. \(8.\)

Answer

3. \(\left( { - \infty ; - 1} \right)\).

Answer

3. \(x = - 2\).

Answer

4. \(y = 3\).

Answer

2. \(\left[ {1; + \infty } \right)\).

Answer

1. \(\left( {2; + \infty } \right)\).

Answer

1. \(y = {x^3} - 3{x^2} + 3\).

Answer

4. \(x = 2\).

Answer

1. \(x = 7\).

Answer

4. \(\left( {1;3} \right)\).

Answer

3. \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx - \int\limits_a^b {g\left( x \right)dx} } .\)

Answer

3. \(\int {f\left( x \right)dx} = \frac{{{x^2}}}{2} + \sin x +C.\)

Answer

1. \(V = \int\limits_a^b {{f^2}(x).dx} \)

Answer

4. Phần thực bằng \( - 5\) và Phần ảo bằng \(3i\).

Answer

2. \(w = - 3 - 3i.\)

Answer

1. \(\left| {{z_1} + {z_2}} \right| = \sqrt {13} .\)

Answer

4. \(\left\{ {5;3} \right\}.\)

Answer

3. \({a^3}\).

Answer

4. \({S_{xq}} = 2\pi rl\).

Answer

3. \(V = 16\pi \,\left( {{m^3}} \right)\).

Answer

2. \(\left( {2;\, - 3;\, - 5} \right)\).

Answer

1. \(\overrightarrow {{n_4}} = (1;2;3)\).

Answer

2. \(\frac{{285}}{{748}}\).

Answer

3. \(30^\circ \).

Answer

2. \(\left( {1; + \infty } \right)\).

Answer

1. \({y_{CĐ}} = - 1\).

Answer

1. \(x = 4\)

Answer

1. \(a < 0,b > 0,c < 0,d > 0\)

Answer

2. \(y' = {2^x}.\ln 2\).

Answer

1. \(x > 33.\)

Answer

4. \(11.\)

Answer

1. \(1 - 4i.\)

Answer

2. \(36\,c{m^3}.\)

Answer

2. \(I(2;0;8).\)

Answer

4. \(I\left( { - 1;2; - 4} \right),R = 5\sqrt 2 \).

Answer

3. \(\,\frac{x}{{ - 2}} + \frac{y}{1} + \frac{z}{3} = 1.\)

Answer

4. \(\frac{a}{2}.\)

Answer

3. \(29.\)

Answer

2. \(24\).

Answer

2. \(\frac{2}{3}\).

Answer

1. \(x + 2y + 2z - 6 = 0\)

Answer

2. \(123.\)

Answer

4. \(M - m + 6\).

Answer

1. \(\frac{{\sqrt 2 - 1}}{3}\).

Answer

3. \(T = \frac{{62}}{{25}}\).

Answer

1. \(C_n^5 = \frac{{n!}}{{(n - 5)!}}\).

Question 2

Câu 2:

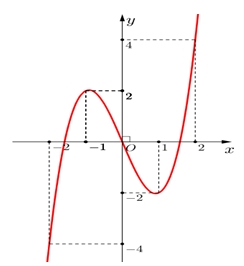
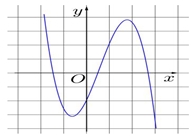
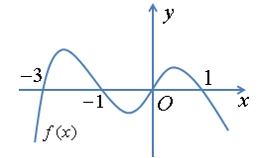
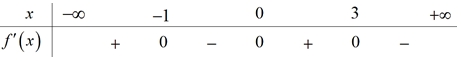Cho hàm số có bảng xét dấu của đạo hàm như sau: Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?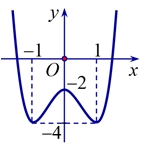

A
1. \(\left( {0; + \infty } \right)\).
B
2. \(\left( { - 1;0} \right)\).
C
3. \(\left( { - \infty ; - 1} \right)\).
D
4. \(\left( { - 1;3} \right)\).

Question 3

Câu 3:

Cho hàm số \(y = a{x^4} + b{x^2} + c,\,\,\left( {a;b;c \in \mathbb{R}} \right)\) có đồ thị là đường cong trong hình bên. Điểm cực đại của hàm số đã cho là Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

A
1. \(x = - 1\).
B
2. \(x = 0\).
C
3. \(x = - 2\).
D
4. \(x = 1\).

Question 4

Câu 4:

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau: Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10 Số điểm cực trị của hàm số đã cho là

A
1. \(1\).
B
2. \(3\).
C
3. \(0\).
D
4. \(2\).

Question 5

Câu 5:

Tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x – 1}}{{x + 1}}\) là đường thẳng có phương trình

A
1. \(y = - 3\).
B
2. \(y = 1\).
C
3. \(y = - 1\).
D
4. \(y = 3\).

Question 6

Câu 6:

Tập xác định của hàm số \(y = {\left( {x – 1} \right)^{\frac{1}{3}}}\) là

A
1. \(\mathbb{R}\).
B
2. \(\left[ {1; + \infty } \right)\).
C
3. \(\left( {1; + \infty } \right)\).
D
4. \(\left( {0; + \infty } \right)\).

Question 7

Câu 7:

Tập xác định của hàm số \(y = {\log _2}\left( {x – 2} \right)\) là

A
1. \(\left( {2; + \infty } \right)\).
B
2. \(\mathbb{R}\).
C
3. \(\left( { - \infty ;2} \right)\).
D
4. \(\left[ {2; + \infty } \right)\).

Question 8

Câu 8:

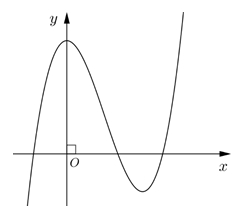
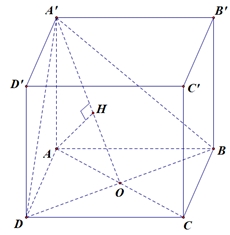Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

A
1. \(y = {x^3} - 3{x^2} + 3\).
B
2. \(y = - {x^3} + 3{x^2} + 1\).
C
3. \(y = - {x^4} + 2{x^2} + 1\).
D
4. \(y = {x^4} - 2{x^2} + 1\).

Question 9

Câu 9:

Nghiệm của phương trình \({5^x} = 25\) là

A
1. \(x = 5\).
B
2. \(x = - 2\).
C
3. \(x = \frac{1}{2}\).
D
4. \(x = 2\).

Question 10

Câu 10:

Nghiệm của phương trình \({\log _3}\left( {x + 2} \right) = 2\) là

A
1. \(x = 7\).
B
2. \(x = 11\).
C
3. \(x = 9\).
D
4. \(x = 6\).

Question 11

Câu 11:

Tập nghiệm của bất phương trình \({\log _2}\left( {x – 1} \right) < 1\) là

A
1. \(\left( {3; + \infty } \right)\).
B
2. \(\left( { - \infty ;3} \right)\).
C
3. \(\left[ {1;3} \right]\).
D
4. \(\left( {1;3} \right)\).

Question 12

Câu 12:

Khẳng định nào sau đây sai?

A
1. \(\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} .\)
B
2. \(\int\limits_a^b {f\left( x \right).g\left( x \right)dx} = \int\limits_a^b {f\left( x \right)dx} .\int\limits_a^b {g\left( x \right)dx} .\)
C
3. \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx - \int\limits_a^b {g\left( x \right)dx} } .\)
D
4. \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx + \int\limits_c^b {f\left( x \right)dx} } ,{\text{ }}\left( {a < c < b} \right).\)

Question 13

Câu 13:

Tìm họ nguyên hàm của hàm số \(f\left( x \right) = x + \cos x.\)

A
1. \(\int {f\left( x \right)dx} = \frac{{{x^2}}}{2} - \sin x +C.\)
B
2. \(\int {f\left( x \right)dx} = 1 - \sin x + C.\)
C
3. \(\int {f\left( x \right)dx} = \frac{{{x^2}}}{2} + \sin x +C.\)
D
4. \(\int {f\left( x \right)dx} = x\sin x + \cos x +C.\)

Question 14

Câu 14:

Nếu \(\int\limits_1^3 {f\left( x \right)dx} = 5,{\text{ }}\int\limits_3^5 {f\left( x \right)dx} = – 2\) thì \(\int\limits_1^5 {\left[ {f\left( x \right) + 1} \right]dx} \) bằng

A
1. \(7.\)
B
2. \(8.\)
C
3. \( - 1.\)
D
4. \(6.\)

Question 15

Câu 15:

Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số , trục và hai đường thẳng , quay xung quan trục .

A
1. \(V = \int\limits_a^b {{f^2}(x).dx} \)
B
2. \(V = \pi \int\limits_a^b {f(x).dx} \)
C
3. \(V = \pi \int\limits_a^b {{f^2}(x).dx} \)
D
4. \(V = \int\limits_a^b {\left| {f(x)} \right|.dx} \)

Question 16

Câu 16:

Cho số phức \(z = 5 – 3i\). Tìm phần thực và phần ảo của số phức\(\overline z \)

A
1. Phần thực bằng \(5\) và Phần ảo bằng \(3\).
B
2. Phần thực bằng \(5\) và Phần ảo bằng \(3i\).
C
3. Phần thực bằng \( - 5\) và Phần ảo bằng \( - 3\).
D
4. Phần thực bằng \( - 5\) và Phần ảo bằng \(3i\).

Question 17

Câu 17:

Cho số phức \(z = 2 + 5i.\) Tìm số phức \(w = iz + \overline z \)

A
1. \(w = 3 + 7i.\)
B
2. \(w = - 3 - 3i.\)
C
3. \(w = 7 - 3i.\)
D
4. \(w = - 7 - 7i\)

Question 18

Câu 18:

Cho hai số phức \({z_1} = 1 + i\) và \({z_2} = 2 – 3i\). Tính môđun của số phức \({z_1} + {z_2}.\)

A
1. \(\left| {{z_1} + {z_2}} \right| = \sqrt {13} .\)
B
2. \(\left| {{z_1} + {z_2}} \right| = \sqrt 5 .\)
C
3. \(\left| {{z_1} + {z_2}} \right| = 1.\)
D
4. \(\left| {{z_1} + {z_2}} \right| = 5.\)

Question 19

Câu 19:

Hình bát diện đều thuộc loại khối đa diện đều nào sau đây

A
1. \(\left\{ {3;3} \right\}.\)
B
2. \(\left\{ {4;3} \right\}.\)
C
3. \(\left\{ {3;4} \right\}.\)
D
4. \(\left\{ {5;3} \right\}.\)

Question 20

Câu 20:

Cho khối chóp có diện tích đáy \(B = 3{a^2}\)và chiều cao \(h = 2a\). Thể tích của khối chóp đã cho bằng

A
1. \(3{a^3}\).
B
2. \(6{a^3}\).
C
3. \({a^3}\).
D
4. \(2{a^3}\).

Question 21

Câu 21:

Cho hình nón có bán kính đáy \(r\) và độ dài đường sinh \(l\). Diện tích xung quanh \({S_{xq}}\) của hình nón đã cho được tính theo công thức nào dưới đây?

A
1. \({S_{xq}} = 4\pi rl\).
B
2. \({S_{xq}} = \pi rl\).
C
3. \({S_{xq}} = \frac{4}{3}\pi rl\).
D
4. \({S_{xq}} = 2\pi rl\).

Question 22

Câu 22:

Thể tích \(V\) của khối cầu có bán kính \(R = 2\,\left( {\text{m}} \right)\) là

A
1. \(V = \frac{{16\pi }}{3}\,\,\left( {{m^3}} \right)\).
B
2. \(V = 32\pi \,\left( {{m^3}} \right)\).
C
3. \(V = 16\pi \,\left( {{m^3}} \right)\).
D
4. \(V = \frac{{32\pi }}{3}\,\left( {{m^3}} \right)\).

Question 23

Câu 23:

Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow a \) biểu diễn của các vectơ đơn vị là \(\overrightarrow a = 2\overrightarrow i – 3\overrightarrow j + 5\overrightarrow k \). Toạ độ của vectơ \(\overrightarrow a \) là

A
1. \(\left( { - 2;\,3;\,5} \right)\).
B
2. \(\left( {2;\, - 3;\, - 5} \right)\).
C
3. \(\left( {2;\, - 3;\,5} \right)\).
D
4. \(\left( {2;\,5;\, - 3} \right)\).

Question 24

Câu 24:

Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):x + 2y + 3z + 4 = 0\). Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left( P \right)\)?

A
1. \(\overrightarrow {{n_4}} = (1;2;3)\).
B
2. \(\overrightarrow {{n_2}} = ( - 1; - 2;3)\).
C
3. \(\overrightarrow {{n_1}} = (1;2;4)\).
D
4. \(\overrightarrow {{n_3}} = (2;3;4)\).

Question 25

Câu 25:

Một lớp học có \(20\) học sinh nam và \(15\) học sinh nữ. Giáo viên chọn ngẫu nhiên \(4\) học sinh đi test Covid. Tính xác suất để \(4\) học sinh được chọn có \(2\) nam và \(2\) nữ.

A
1. \(\frac{{59}}{{5236}}\).
B
2. \(\frac{{285}}{{748}}\).
C
3. \(\frac{{59}}{{10472}}\).
D
4. \(\frac{{855}}{{2618}}\).

Question 26

Câu 26:

Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác đều cạnh bằng \(a\sqrt 3 \) và cạnh bên bằng \(a\). Góc giữa đường thẳng \(BB'\) và \(AC'\) bằng

A
1. \(45^\circ \).
B
2. \(90^\circ \).
C
3. \(30^\circ \).
D
4. \(60^\circ \).

Question 27

Câu 27:

Cho hàm số \(y = f(x)\) có đồ thị là đường cong trong hình vẽ bên.

Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

Hàm số \(f(x)\) đồng biến trên khoảng nào dưới đây?

A
1. \(\left( {0; + \infty } \right)\).
B
2. \(\left( {1; + \infty } \right)\).
C
3. \(\left( { - 1;1} \right)\).
D
4. \(\left( { - 2;0} \right)\)

Question 28

Câu 28:

Tìm giá trị cực đại \({y_{CĐ}}\) của hàm số \(y = {x^3} – 3x + 2\)

A
1. \({y_{CĐ}} = - 1\).
B
2. \({y_{CĐ}} = 4\).
C
3. \({y_{CĐ}} = 1\).
D
4. \({y_{CĐ}} = 0\).

Question 29

Câu 29:

Trên đoạn \(\left[ {1;4} \right]\), hàm số \(y = {x^4} – 8{x^2} + 13\) đạt giá trị nhỏ nhất tại điểm

A
1. \(x = 4\)
B
2. \(x = 1\).
C
3. \(x = 3\).
D
4. \(x = 2\).

Question 30

Câu 30:

Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên dưới. Mệnh đề nào dưới đây đúng ? Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

A
1. \(a < 0,b > 0,c < 0,d > 0\)
B
2. \(a > 0,b < 0,c < 0,d > 0\).
C
3. \(a < 0,b < 0,c > 0,d < 0\).
D
4. \(a < 0,b > 0,c > 0,d < 0\)..

Question 31

Câu 31:

Tính đạo hàm của hàm số \(y = {2^x}\)

A
1. \(y' = x{.2^{x - 1}}\).
B
2. \(y' = {2^x}.\ln 2\).
C
3. \(y' = \frac{{{2^x}}}{{\ln 2}}\).
D
4. \(y' = {2^x}\)

Question 32

Câu 32:

Giải bất phương trình \({\log _2}(x – 1) > 5.\)

A
1. \(x > 33.\)
B
2. \(x < 33.\)
C
3. \(x < 11.\)
D
4. \(x > 11.\)

Question 33

Câu 33:

Nếu \(\int\limits_0^2 {f\left( x \right){\text{d}}x} = 5\) thì \(\int\limits_0^2 {\left[ {2f\left( t \right) + 1} \right]{\text{dt}}} \)bằng

A
1. \(12.\)
B
2. \(10.\)
C
3. \(9.\)
D
4. \(11.\)

Question 34

Câu 34:

Cho hai số phức \({z_1} = 2 – 3i\) và\({z_2} = – 1 + i\). Số phức \({z_1} – {z_2}\) bằng

A
1. \(1 - 4i.\)
B
2. \(1 - 2i.\)
C
3. \(3 - 2i.\)
D
4. \(3 - 4i.\)

Question 35

Câu 35:

Cho số phức \(z\) thỏa mãn \(z\left( {1 + i} \right) = 3 – 5i\) có phần ảo là

A
1. \( - 5.\)
B
2. \(4.\)
C
3. \(1.\)
D
4. \( - 4.\)

Question 36

Câu 36:

Cho tứ diện \(OABC\) có ba cạnh\(OA\), \(OB\), \(OC\) đôi một vuông góc và đều bằng \(6cm\). Tính thể tích tứ diện \(OABC\) là

A
1. \(6\,c{m^3}.\)
B
2. \(36\,c{m^3}.\)
C
3. \(108\,c{m^3}.\)
D
4. \(72\,c{m^3}.\)

Question 37

Câu 37:

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm \(A(3; – 2;3),\,\,B( – 1;2;5)\). Tìm toạ độ trung điểm I của đoạn thẳng \(AB\)?

A
1. \(I(2; - 2; - 1).\)
B
2. \(I(2;0;8).\)
C
3. \(I(1;0;4).\)
D
4. \(I( - 2;2;1).\)

Question 38

Câu 38:

Trong không gian với hệ tọa độ \(Oxyz\), tìm tọa độ tâm \(I\) và bán kính \(R\) của mặt cầu \({\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z – 4} \right)^2} = 20\)

A
1. \(I\left( {1; - 2;4} \right),R = 2\sqrt 5 \).
B
2. \(I\left( {1; - 2;4} \right),R = 20\).
C
3. \(I\left( { - 1;2; - 4} \right),R = 2\sqrt 5 \).
D
4. \(I\left( { - 1;2; - 4} \right),R = 5\sqrt 2 \).

Question 39

Câu 39:

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm \(A(1;0;0),\,\,B(0; – 2;0)\) và \(C(0;0;3)\). Phương trình nào dưới đây là phương trình của mặt phẳng \((ABC)\)?

A
1. \(\,\frac{x}{3} + \frac{y}{1} + \frac{z}{{ - 2}} = 1.\)
B
2. \(\,\frac{x}{1} + \frac{y}{{ - 2}} + \frac{z}{3} = 1.\)
C
3. \(\,\frac{x}{{ - 2}} + \frac{y}{1} + \frac{z}{3} = 1.\)
D
4. \(\,\frac{x}{3} + \frac{y}{{ - 2}} + \frac{z}{1} = 1.\)

Question 40

Câu 40:

Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 2a\), góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\) bằng \({30^0}\). Khoảng cách từ A đến mặt phẳng \(\left( {A'BD} \right)\) bằng

A
1. \(\frac{{2a\sqrt {13} }}{{13}}.\)
B
2. \(\frac{a}{4} \cdot \)
C
3. \(\frac{{a\sqrt {14} }}{7} \cdot \)
D
4. \(\frac{a}{2}.\)

Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

Gọi \(O\) là giao điểm của \(AC\) và \(BD\).

Ta có

\(\left\{ \begin{array}{l}

BD \bot AO\\

BD \bot AA’

\end{array} \right. \Rightarrow BD \bot \left( {AOA’} \right) \Rightarrow A’O \bot BD\).

Khi đó

\(\left\{ \begin{array}{l}

\left( {AOA’} \right) \bot \left( {A’BD} \right)\\

\left( {AOA’} \right) \cap \left( {A’BD} \right) = A’O\\

Trong\,\left( {AOA’} \right):AH \bot A’O

\end{array} \right.\).

Question 41

Câu 41:

Cho hàm số \(y = f\left( x \right) = \left\{ \begin{gathered} {e^x} + 1{\text{ khi }}x \geqslant 0 \hfill \\ {x^2} – 2x + 2{\text{ khi }}x < 0 \hfill \\ \end{gathered} \right.\). Tích phân \(I = \int\limits_{1/e}^{{e^2}} {\frac{{f\left( {\ln x - 1} \right)}}{x}} dx = \frac{a}{b} + ce\) biết \(a,b,c \in Z\) và \(\frac{a}{b}\) tối giản. Tính \(a + b + c?\)

A
1. \(27.\)
B
2. \(36.\)
C
3. \(29.\)
D
4. \(35.\)

Xét \(I = \int\limits_{1/e}^{{e^2}} {\frac{{f\left( {\ln x – 1} \right)}}{x}} dx\).Đặt \(u = \ln x – 1 \Rightarrow du = \frac{1}{x}dx\). Đổi cận \(\left\{ \begin{gathered} x = \frac{1}{e} \Rightarrow u = – 2 \hfill \\ x = {e^2} \Rightarrow u = 1 \hfill \\ \end{gathered} \right.\).Khi đó \(I = \int\limits_{ – 2}^1 {f\left( u \right)du} = \int\limits_{ – 2}^1 {f\left( x \right)dx} = \int\limits_{ – 2}^0 {f\left( x \right)dx} + \int\limits_0^1 {f\left( x \right)dx} \)\( = \int\limits_{ – 2}^0 {\left( {{x^2} – 2x + 2} \right)dx} + \int\limits_0^1 {\left( {{e^x} + 1} \right)dx} \)\( = \left. {\left( {\frac{1}{3}{x^3} – {x^2} + 2x} \right)} \right|_{ – 2}^0 + \left. {\left( {{e^x} + x} \right)} \right|_0^1 = \frac{{32}}{3} + e\).Do đó \(a = 32,b = 3,c = 1 \Rightarrow a + b + c = 36\).

Question 42

Câu 42:

Cho các số phức \(z,w\) thỏa mãn \(\left| z \right| = 2\), \(\left| {w – 3 + 2i} \right| = 1\) khi đó \(\left| {{z^2} – 2zw – 4} \right|\) đạt giá trị lớn nhấtbằng

A
1. \(20\).
B
2. \(24\).
C
3. \(16\).
D
4. \(4 + 4\sqrt {13} \).

Gọi \(M\left( {x;\,y} \right)\) là điểm biểu diễn của số phức \(z = x + iy\,\left( {x,y \in \mathbb{R}} \right)\), \(E\) là điểm biểu diễn của số phức \(w\). Từ giả thiết suy ra \(M\) thuộc đường tròn tâm \(O\left( {0;\,0} \right)\), bán kính \({R_1} = 2\); \(E\) thuộc đường tròn tâm \(I\left( {3;\, – 2} \right)\), bán kính \({R_2} = 1\);Ta có\(\begin{gathered} P = \left| {{z^2} – 2zw – 4} \right| = \left| {{z^2} – 2zw – {{\left| z \right|}^2}} \right| = \left| {{z^2} – 2zw – z.\overline z } \right| = \left| z \right|.\left| {z – 2w – \overline z } \right| \hfill \\ \,\,\,\,\, = 2.\left| {z – 2w – \overline z } \right| = 2.\left| {2y – 2w} \right| = 4\left| {y – w} \right| = 4KE \geqslant HN \hfill \\ \end{gathered} \)\( \Rightarrow P \geqslant 4\left( {HI + {R_2}} \right) \Leftrightarrow P \geqslant 24\)Trong đó \(K\left( {0;\,y} \right)\), \( – 2 \leqslant y \leqslant 2\), \(H\left( {0;\,2} \right),\,N\) là giao điểm của đường tròn \(\left( I \right)\) và đường thẳng \(IH\), \({x_N} > 3\).

Question 43

Câu 43:

Trên bàn có một cố nước hình trụ chứa đầy nước, có chiều cao bằng \(3\) lần đường kính của đáy; Một viên bi và một khối nón đều bằng thuỷ tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của đường tròn đáy cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nón nằm trên mặt cầu ( như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu. 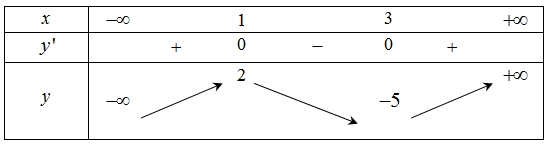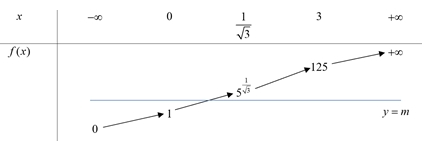Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

A
1. \(\frac{4}{9}\).
B
2. \(\frac{2}{3}\).
C
3. \(\frac{5}{9}\).
D
4. \(\frac{1}{2}\).

Gọi bán kính đáy của cốc nước hình trụ là \(r\), suy ra chiều cao cốc nước bằng \(6r\).Khi đó thể tích khối trụ bằng lượng nước ban đầu: \({V_1} = \pi {r^2}.6r = 6\pi {r^3}\).Thể tích khối cầu bằng: \({V_2} = \frac{4}{3}\pi {r^3}\).Khối nón có chiều cao bằng \(h = 6r – 2r = 4r\) nên thể tích bằng \({V_3} = \frac{1}{3}\pi {r^2}.h = \frac{1}{3}\pi {r^2}.4r = \frac{4}{3}\pi {r^3}\).Phần thể tích nước tràn ra đúng bằng thể tích chiếm chỗ của khối cầu và khối nón.Suy ra thể tích lượng nước còn lại bằng: \(V = {V_1} – \left( {{V_2} + {V_3}} \right) = 6\pi {r^3} – \left( {\frac{4}{3}\pi {r^3} + \frac{4}{3}\pi {r^3}} \right) = \frac{{10}}{3}\pi {r^3}\).Vậy tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu bằng \(\frac{{\frac{{10}}{3}\pi {r^3}}}{{6\pi {r^3}}} = \frac{5}{9}\).

Question 44

Câu 44:

Trong không gian Oxyz, cho mặt phẳng \((P)\) song song và cách mặt phẳng `\((Q):x + 2y + 2z – 3 = 0\) một khoảng bằng 1 và \((P)\) không qua gốc tọa độ O. Phương trình của mặt phẳng \((P)\) là

A
1. \(x + 2y + 2z - 6 = 0\)
B
2. \(x + 2y + 2z + 3 = 0\)
C
3. \(x + 2y + 2z + 1 = 0\)
D
4. \(x + 2y + 2z = 0\)

Mặt phẳng \((P)\) song song với mặt phẳng \((Q):x + 2y + 2z – 3 = 0\) nên phương trình mp\((P):\,x + 2y + 2{\text{z}} + d = 0\).\(A\left( {3,0,0} \right) \in \left( Q \right)\).Mặt phẳng \((P)\) cách mặt phẳng `\((Q):x + 2y + 2z – 3 = 0\) một khoảng bằng 1 \( \Rightarrow d\left( {A,\left( P \right)} \right) = 1 \Leftrightarrow \frac{{\left| {3 + d} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} = 1 \Leftrightarrow \left| {d + 3} \right| = 3 \Leftrightarrow \left[ \begin{gathered} d = – 6 \hfill \\ d = 0 \hfill \\ \end{gathered} \right.\).Vì \((P)\) không qua gốc tọa độ O nên \(d \ne 0\) \( \Rightarrow d = – 6\).Vậy pt mặt phẳng \(\left( P \right)\) : \(x + 2y + 2z – 6 = 0\).

Question 45

Câu 45:

Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\)và có đồ thị có 3 điểm cực trị như hình vẽ dưới đây. Số điểm cực trị của hàm số \(g(x) = f({x^3} – 3x + 2)\) là: Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

A
1. \(11.\)
B
2. \(7.\)
C
3. \(9.\)
D
4. \(5.\)

Ta có: \(g'\left( x \right) = \left( {3{x^2} – 3} \right)f'\left( {{x^3} – 3x + 2} \right)\), \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered} 3{x^3} – 3 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\ f'\left( {{x^3} – 3x + 2} \right) = 0\,\,\,(2) \hfill \\ \end{gathered} \right.\)\((1) \Leftrightarrow x = \pm 1\).Dựa vào đồ thị đã cho thì \((2) \Leftrightarrow \left[ \begin{gathered} {x^3} – 3x + 2 = a \in \left( { – 3; – 1} \right) \hfill \\ {x^3} – 3x + 2 = b \in \left( { – 1;0} \right) \hfill \\ {x^3} – 3x + 2 = c \in \left( {0;1} \right) \hfill \\ \end{gathered} \right.\)Xét hàm số \(g\left( x \right) = {x^3} – 3x + 2 \Rightarrow g'\left( x \right) = 3{x^2} – 3 = 0 \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x = – 1 \hfill \\ \end{gathered} \right.\).Ta có bảng biến thiên của hàm số \(g\left( x \right)\)Dựa vào bảng biến thiên ta có:phương trình \({x^3} – 3x + 2 = a \in \left( { – 3; – 1} \right)\) có 1 nghiệm đơnphương trình \({x^3} – 3x + 2 = b \in \left( { – 1;0} \right)\) có 1 nghiệm đơnphương trình \({x^3} – 3x + 2 = c \in \left( {0;1} \right)\) có 3 nghiệm phân biệtTa có \(5\) nghiệm đơn trên đôi một khác nhau và khác \( \pm 1\). Vậy hàm số có 7 điểm cực trị.

Question 46

Câu 46:

Cho phương trình \(\left( {2\log _3^2x – {{\log }_3}x – 1} \right)\sqrt {{5^x} – m} = 0\) (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng 2 nghiệm phân biệt?

A
1. \(122.\)
B
2. \(123.\)
C
3. \(124.\)
D
4. \(125.\)

Điều kiện: \(\left\{ \begin{gathered} x > 0 \hfill \\ {5^x} – m \geqslant 0\,\,\left( {m > 0} \right) \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ x \geqslant {\log _5}m \hfill \\ \end{gathered} \right.\).\(\left( {2\log _3^2x – {{\log }_3}x – 1} \right)\sqrt {{5^x} – m} = 0\) (1)\( \Leftrightarrow \left[ \begin{gathered} 2\log _3^2x – {\log _3}x – 1 = 0 \hfill \\ {5^x} – m = 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = 3,x = \frac{1}{{\sqrt 3 }} \hfill \\ f\left( x \right) = {5^x} = m \hfill \\ \end{gathered} \right.\).Xét \(f\left( x \right) = {5^x}\) hàm số đồng biến trên \(\mathbb{R}\). Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

Dựa vào bảng biến thiên, để phương trình có hai nghiệm phân biệt thì\(\left[ \begin{gathered} m = 1 \hfill \\ {5^{\frac{1}{{\sqrt 3 }}}} \leqslant m < 125 \hfill \\ \end{gathered} \right.\), \(m \in {\mathbb{Z}_ + }\) \( \Rightarrow \left[ \begin{gathered} 0 < m \leqslant 1 \hfill \\ 3 \leqslant m \leqslant 124 \hfill \\ \end{gathered} \right.\). Nên có 123 giá trị m thoả mãn.

Question 47

Câu 47:

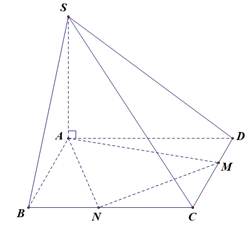Cho hàm số \(y = f\left( x \right)\)xác định và liên tục trên đoạn\(\left[ { – 3;3} \right]\). Biết diện tích hình phẳng \({S_1},{S_2}\) giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = – x – 1\) lần lượt là \(M,m\). Tính tích phân \(\int\limits_{ – 3}^3 {f\left( x \right)dx} \) bằng? Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

A
1. \(m - M - 6\).
B
2. \(6 + m - M\).
C
3. \(6 - m - M\).
D
4. \(M - m + 6\).

\(M = \int\limits_{ – 3}^1 {\left( { – x – 1 – f\left( x \right)} \right)} dx \Leftrightarrow M = \int\limits_{ – 3}^1 {\left( { – x – 1} \right)} dx – \int\limits_{ – 3}^1 {f\left( x \right)} dx \Leftrightarrow \int\limits_{ – 3}^1 {f\left( x \right)} dx = – M\)\(m = \int\limits_1^3 {\left( {f\left( x \right) + x + 1} \right)} dx \Leftrightarrow m = \int\limits_1^3 {\left( {x + 1} \right)} dx + \int\limits_1^3 {f\left( x \right)} dx \Leftrightarrow \int\limits_1^3 {f\left( x \right)} dx = m – 6\).\(\int\limits_{ – 3}^3 {f(x)dx} = \int\limits_{ – 3}^1 {f(x)dx} + \int\limits_1^3 {f(x)dx} = – M + m – 6\).

Question 48

Câu 48:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(AB = 1\), cạnh bên \(SA = 1\) và vuông góc với mặt phẳng đáy \((ABCD)\). Kí hiệu \(M\) là điểm di động trên đoạn \(CD\) và \(N\) là điểm di động trên đoạn \(CB\) sao cho góc \(MAN\) bằng \(45^\circ \). Thể tích nhỏ nhất của khối chóp \(S.AMN\) là

A
1. \(\frac{{\sqrt 2 - 1}}{3}\).
B
2. \(\frac{{\sqrt 2 + 1}}{9}\).
C
3. \(\frac{{\sqrt 2 - 1}}{9}\).
D
4. \(\frac{{\sqrt 2 + 1}}{6}\).

Đặt \(\widehat {BAN} = \alpha \) suy ra \(\widehat {MAD} = 45^\circ – \alpha \).Khi đó \(AN = \frac{{AB}}{{\cos \alpha }} = \frac{1}{{\cos \alpha }}\) và \(AM = \frac{{AD}}{{\cos \left( {45^\circ – \alpha } \right)}} = \frac{1}{{\cos \left( {45^\circ – \alpha } \right)}}\).Do đó diện tích tam giác \(AMN\) bằng \({B_{AMN}} = \frac{1}{2}AM.AN.\sin 45^\circ = \frac{{\sqrt 2 }}{4}.\frac{1}{{\cos \alpha .\cos \left( {45^\circ – \alpha } \right)}}\).Thể tích \(S.AMN\) bằng \({V_{S.AMN}} = \frac{1}{3}{B_{AMN}}.SA = \frac{{\sqrt 2 }}{{12}}.\frac{1}{{\cos \alpha .\cos \left( {45^\circ – \alpha } \right)}}\).Thể tích của khối chóp \(S.AMN\) nhỏ nhất khi \(\cos \alpha .\cos \left( {45^\circ – \alpha } \right)\) lớn nhất.Xét \(f\left( \alpha \right) = \cos \alpha .\cos \left( {45^\circ – \alpha } \right)\) trong đó \(\alpha \in \left( {0^\circ ;45^\circ } \right)\).Ta có \(f'\left( \alpha \right) = \sin \left( {45^\circ – 2\alpha } \right)\); \(f'\left( \alpha \right) = 0 \Leftrightarrow \alpha = \frac{{45^\circ }}{2}\).Bảng biến thiên 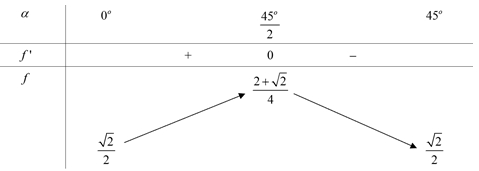Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

Từ bảng biến thiên ta có \(\mathop {\max }\limits_{\alpha \in \left[ {0^\circ ;45^\circ } \right]} f\left( \alpha \right) = f\left( {\frac{{45^\circ }}{2}} \right) = \frac{{2 + \sqrt 2 }}{4}\).Vậy thể tích nhỏ nhất của \(S.AMN\) bằng \({V_{S.AMN}} = \frac{{\sqrt 2 }}{{12}}.\frac{1}{{\frac{{2 + \sqrt 2 }}{4}}} = \frac{{\sqrt 2 – 1}}{3}\).

Question 49

Câu 49:

Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 2} \right)^2} = 9\) và điểm \(M(1;3; – 1)\), biết rằng các tiếp điểm của các tiếp tuyến kẻ từ \(M\) tới mặt cầu đã cho luôn thuộc một đường tròn \(\left( C \right)\) có tâm \(J\left( {a;b;c} \right)\). Giá trị \(T = 2a + b + c\) bằng

A
1. \(T = \frac{{84}}{{25}}\).
B
2. \(T = \frac{{134}}{{25}}\).
C
3. \(T = \frac{{62}}{{25}}\).
D
4. \(T = \frac{{116}}{{25}}\).

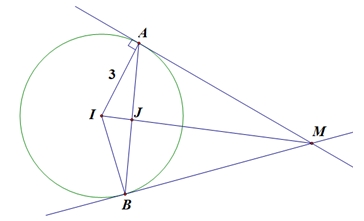Mặt cầu \(\left( S \right)\) có tâm \(I\left( {1; – 1;2} \right),R = 3,IM = 5\).Gọi \(A,B\) là các tiếp điểm. Khi đó các tiếp điểm của các tiếp tuyến kẻ từ \(M\) tới mặt cầu đường tròn \(\left( C \right)\) có tâm \(J\) là trung điểm của dây \(AB\).Xét \(\Delta IAM\) có \(I{A^2} = IJ.IM \Leftrightarrow I{J^2} = \frac{9}{{25}}\).Phương trình \(IM:\left\{ \begin{gathered} x = 1 \hfill \\ y = – 1 + 4t \hfill \\ z = 2 – 3t \hfill \\ \end{gathered} \right.\). Vì \(J \in IM \Rightarrow J\left( {1;4t – 1;2 – 3t} \right),t \in \mathbb{R}\).Ta có: \(I{J^2} = \frac{9}{{25}} \Leftrightarrow {\left( {4t} \right)^2} + {\left( { – 3t} \right)^2} = \frac{{81}}{{25}} \Leftrightarrow {t^2} = \frac{{81}}{{{{25}^2}}} \Rightarrow \left[ \begin{gathered} t = \frac{9}{{25}} \hfill \\ t = – \frac{9}{{25}} \hfill \\ \end{gathered} \right.\).+) Với \(t = \frac{9}{{25}} \Rightarrow J\left( {1;\frac{{11}}{{25}};\frac{{23}}{{25}}} \right) \Rightarrow T = 2a + b + c = \frac{{84}}{{25}}\).+) Với \(t = – \frac{9}{{25}} \Rightarrow J\left( {1;\frac{{ – 61}}{{25}};\frac{{77}}{{25}}} \right) \Rightarrow T = 2a + b + c = \frac{{66}}{{25}}\). (loại)

Question 50

Câu 50:

Với \(n\) là số nguyên dương bất kỳ, \(n \geqslant 5\), công thức nào sau đây đúng?

A
1. \(C_n^5 = \frac{{n!}}{{(n - 5)!}}\).
B
2. \(C_n^5 = \frac{{5!(n - 5)!}}{{n!}}\).
C
3. \(C_n^5 = \frac{{(n - 5)!}}{{n!}}\).
D
4. \(C_n^5 = \frac{{n!}}{{5!(n - 5)!}}\).

Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

Đề Kiểm Tra: Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

Các lựa chọn đã được chọn:

Đáp án: Đề Luyện Thi TN THPT Năm 2023 Môn Toán Online-Đề 10

Trắc Nghiệm Liên Quan

Đề Luyện Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 9

Đề Luyện Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 8

Đề Ôn Thi Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 7

Đề Ôn Thi Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 6

Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 5

Đề Luyện Thi TN THPT 2023 Môn Toán Online-Đề 11

Đề Ôn Thi TN THPT 2023 Môn Toán Online-Đề 12

Đề Ôn Thi TN THPT Năm 2023 Môn Toán Online-Đề 13

Đề Ôn Thi TN THPT Năm 2023 Toán Online-Đề 14

Đề Kiểm Tra Giữa Học Kì 1 Môn Toán 12 Online-Đề 1

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN