
Danh Mục Sách
- Thiếu nhi
- Giáo khoa - Tham khảo
- Văn học
- Tâm lý - Kỹ năng sống
- Manga - Comic
- Sách học ngoại ngữ
- Kinh Tế
- Khoa học kỹ thuật
- Lịch Sử - Địa Lý - Tôn Giáo
- Nuôi Dạy Con
- Chính Trị - Pháp Lý - Triết Học
- Tiểu Sử Hồi Ký
- Đam Mỹ
- Nữ Công Gia Chánh
- Văn Hóa - Nghệ Thuật - Du Lịch
- Phong Thủy - Kinh Dịch
- Từ điển
- Âm Nhạc - Mỹ Thuật - Thời Trang
- Thể Dục Thể thao - Giải Trí
- Báo - Tạp Chí
- Giáo trình
- Làm Vườn - Thú Nuôi
- Mystery Box
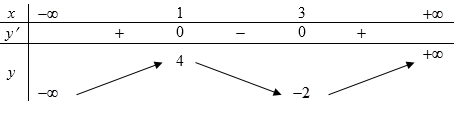 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?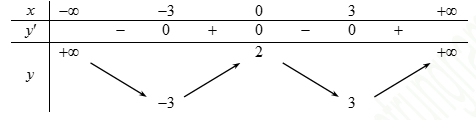 Tìm tất cả giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) – m = 0\) có bốn nghiệm phân biệt.
Tìm tất cả giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) – m = 0\) có bốn nghiệm phân biệt.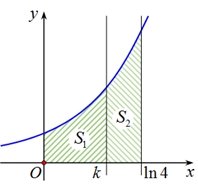 Tìm \(k\) để \({S_1} = 2{S_2}\).
Tìm \(k\) để \({S_1} = 2{S_2}\).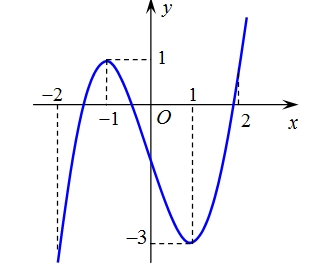 Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?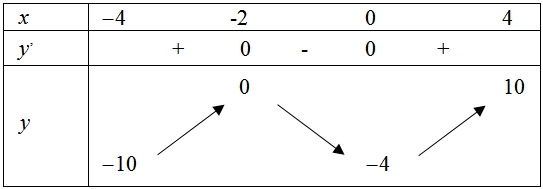 Phát biểu nào sau đây đúng?
Phát biểu nào sau đây đúng?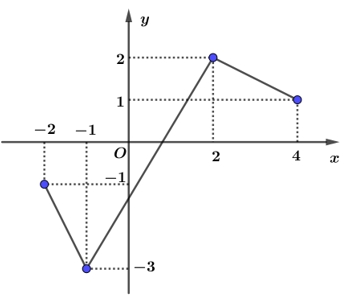 Tìm \(\mathop {\max }\limits_{\left[ { – 2;{\rm{4}}} \right]} \left| {f\left( x \right)} \right|\).
Tìm \(\mathop {\max }\limits_{\left[ { – 2;{\rm{4}}} \right]} \left| {f\left( x \right)} \right|\).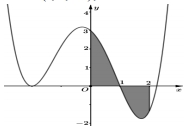 Diện tích của hình phẳng giới hạn bới đồ thị \(\left( C \right)\) và hai đường thẳng \(x = 0\), \(x = 2\)(phần tô đen) là
Diện tích của hình phẳng giới hạn bới đồ thị \(\left( C \right)\) và hai đường thẳng \(x = 0\), \(x = 2\)(phần tô đen) là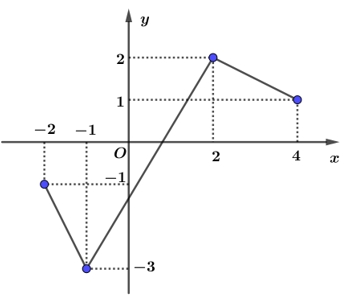 Hỏi hàm số đó là hàm số nào?
Hỏi hàm số đó là hàm số nào?