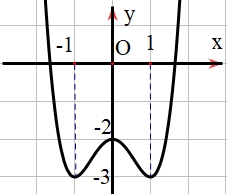
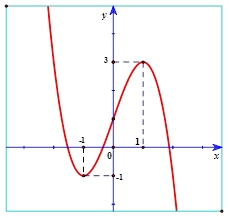Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1

Question 1

Câu 1:

Cho số phức \(z = 3 – 4i\). Môđun của \(z\) bằng

A
1. \( - 1\).
B
2. \(7\).
C
3. \(5\).
D
4. \(25\).

Answer

4. \(25\).

Question 2

Câu 2:

Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z – 5} \right)^2} = 9\). Tìm tọa độ tâm của mặt cầu \(\left( S \right).\)

A
1. \(\left( {1; - 2; - 5} \right).\)
B
2. \(\left( {1;2;5} \right).\)
C
3. \(\left( {1; - 2;5} \right).\)
D
4. \(\left( { - 1; - 2;5} \right).\)

Answer

2. \(\left( {1;2;5} \right).\)

Question 3

Câu 3:

Điểm nào dưới đây thuộc đồ thị hàm số \(y = {x^4} – 2{x^2} – 1\) ?

A
1. Điểm \(M\left( {2; - 2} \right)\)
B
2. Điểm \(N\left( { - 1; - 2} \right)\)
C
3. Điểm \(P\left( {0;1} \right)\)
D
4. Điểm \(Q\left( { - 2;4} \right)\)

Answer

2. Điểm \(N\left( { - 1; - 2} \right)\)

Question 4

Câu 4:

Một khối cầu có bán kính \(2R\) thì có thể tích \(V\) bằng bao nhiêu?

A
1. \(V = \frac{{32\pi {R^3}}}{3}\).
B
2. \(V = \frac{{4\pi {R^3}}}{3}\).
C
3. \(V = \frac{{24\pi {R^3}}}{3}\).
D
4. \(V = 4\pi {R^2}\).

Answer

3. \(V = \frac{{24\pi {R^3}}}{3}\).

Question 5

Câu 5:

Nguyên hàm của hàm số \(f\left( x \right) = {x^3} + 3x + 2\) là hàm số nào trong các hàm số sau ?

A
1. \(F\left( x \right) = 3{x^2} + 3x + C\).
B
2. \(F\left( x \right) = \frac{{{x^4}}}{3} + 3{x^2} + 2x + C\).
C
3. \(F\left( x \right) = \frac{{{x^4}}}{4} + \frac{{3{x^2}}}{2} + 2x + C\).
D
4. \(F\left( x \right) = \frac{{{x^4}}}{4} + \frac{{{x^2}}}{2} + 2x + C\).

Answer

3. \(F\left( x \right) = \frac{{{x^4}}}{4} + \frac{{3{x^2}}}{2} + 2x + C\).

Question 6

Câu 6:

Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Tìm kết luận đúng?

A
1. Hàm số \(f\left( x \right)\) có giá trị cực tiểu là \(0\).
B
2. Hàm số \(f\left( x \right)\) có điểm cực đại là \(x = 4\).
C
3. Hàm số \(f\left( x \right)\) có giá trị cực đại là \( - 1\).
D
4. Hàm số \(f\left( x \right)\) có điểm cực tiểu là \(x = 2\).

Answer

4. Hàm số \(f\left( x \right)\) có điểm cực tiểu là \(x = 2\).

Question 7

Câu 7:

Tìm tập nghiệm \(S\)của bất phương trình \({\left( {\frac{1}{2}} \right)^x} > 8.\)

A
1. \(S = (3; + \infty )\).
B
2. \(S = ( - \infty ; - 3)\).
C
3. \(S = ( - \infty ;3)\).
D
4. \(S = ( - 3; + \infty )\).

Answer

3. \(S = ( - \infty ;3)\).

Question 8

Câu 8:

Khối lập phương có thể tích bằng \(8\). Tính độ dài cạnh của hình lập phương đó

A
1. \(\frac{8}{3}\).
B
2. \(2\).
C
3. \(\frac{2}{3}\).
D
4. \(4\).

Answer

3. \(D = \mathbb{R}\).

Answer

3. \(\left\{ {0;3} \right\}.\)

Answer

3. \(I = - 28\).

Answer

1. \(z = - 4 + 5i\).

Answer

4. \(\vec n = \left( { - 2;\, - 1;\,1} \right)\).

Answer

1. \(\overrightarrow a \left( { - 1;2; - 3} \right)\).

Answer

2. \(\left( {2; - 3} \right)\).

Answer

4. \(x = 2\) và \(y = 1\).

Answer

1. \(I = - 3\).

Answer

2. \(y = {x^4} - 2{x^2} - 2\).

Answer

1. \(M(5;\,5;\,5)\)

Answer

3. \(104.\)

Answer

1. \(\sqrt 3 {a^3}\).

Answer

1. \(y' = x{\pi ^{x - 1}}\).

Answer

4. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).

Answer

4. \(\frac{{16}}{3}\pi {a^3}\).

Answer

3. \(34\) .

Answer

2. \(403.\)

Answer

4. \(\int {\sin 2xdx = 2\cos 2x + C,C \in \mathbb{R}} \).

Answer

2. \( - 4\).

Answer

2. \(y = {x^3} + 4{x^2} + 3x - 1\) .

Answer

2. \(\log a + 2\log b\).

Answer

2. \(60^\circ \).

Answer

1. \(2x + y + 3z - 4 = 0\).

Answer

4. \(h = a\sqrt 3 \).

Answer

4. \(0,2\).

Answer

1. \(d:\frac{{x - 2}}{2} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 1}}{3}\)

Answer

1. \(12\).

Answer

1. \(\frac{{\sqrt 2 }}{3}{a^3}\).

Answer

3. \(M = 9\)

Answer

1. \(a + c < b + d\).

Answer

1. \(\Delta :\left\{ \begin{gathered} x = 2 + 2t \hfill \\ y = - 2 - t \hfill \\ z = 0 \hfill \\ \end{gathered} \right.\).

Answer

4. \(V = \frac{{\pi {a^3}}}{2}\).

Answer

3. \(S = 0\).

Answer

2. \(\sqrt 7 \).

Question 9

Câu 9:

Tập xác định \(D\) của hàm số \(y = {\left( {2x – 1} \right)^\pi }\).

A
1. \(D = \left( {\frac{1}{2};\,\, + \infty } \right)\).
B
2. \(D = \left[ {\frac{1}{2};\,\, + \,\infty } \right)\).
C
3. \(D = \mathbb{R}\).
D
4. \(D = \,\,\mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\).

Question 10

Câu 10:

Tập nghiệm của phương trình \({\log _3}\left( {{x^2} – 3x + 3} \right) = 1\) là

A
1. \(\left\{ 3 \right\}.\)
B
2. \(\left\{ { - 3;0} \right\}.\)
C
3. \(\left\{ {0;3} \right\}.\)
D
4. \(\left\{ 0 \right\}.\)

Question 11

Câu 11:

Cho \(\int\limits_a^c {f\left( x \right){\text{d}}x} = 17\) và \(\int\limits_b^c {f\left( x \right){\text{d}}x} = – 11\) với \(a < b < c\). Tính \(I = \int\limits_a^b {f\left( x \right){\text{d}}x} \).

A
1. \(I = - 6\).
B
2. \(I = 6\).
C
3. \(I = - 28\).
D
4. \(I = 28\).

Question 12

Câu 12:

Cho hai số phức \({z_1} = 1 – 2i\), \({z_2} = – 2 + i\). Tìm số phức \(z = {z_1}{z_2}\).

A
1. \(z = - 4 + 5i\).
B
2. \(z = 4 - 5i\).
C
3. \(z = - 5i\).
D
4. \(z = 5i\).

Question 13

Câu 13:

Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):2x + y – 1 = 0\). Mặt phẳng \(\left( P \right)\) có một vectơ pháp tuyến là

A
1. \(\vec n = \left( {1;\,2;\,0} \right)\).
B
2. \(\vec n = \left( {2;\,1;\, - 1} \right)\).
C
3. \(\vec n = \left( {2;\,1;\,0} \right)\).
D
4. \(\vec n = \left( { - 2;\, - 1;\,1} \right)\).

Question 14

Câu 14:

Trong không gian với trục hệ tọa độ \(Oxyz\), cho \(\overrightarrow a = – \overrightarrow i + 2\overrightarrow j – 3\overrightarrow k .\) Tọa độ của vectơ \(\overrightarrow a \) là:

A
1. \(\overrightarrow a \left( { - 1;2; - 3} \right)\).
B
2. \(\overrightarrow a \left( {2; - 3; - 1} \right)\).
C
3. \(\overrightarrow a \left( { - 3;2; - 1} \right)\).
D
4. \(\overrightarrow a \left( {2; - 1; - 3} \right)\).

Question 15

Câu 15:

Số phức \(z = 2 – 3i\)có điểm biểu diễn là

A
1. \(\left( { - 2; - 3} \right)\).
B
2. \(\left( {2; - 3} \right)\).
C
3. \(\left( {2;3} \right)\).
D
4. \(\left( { - 2;3} \right)\).

Question 16

Câu 16:

Đồ thị hàm số \(y = \frac{{2x – 3}}{{x – 1}}\) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là

A
1. \(x = 1\) và \(y = 2\).
B
2. \(x = - 1\) và \(y = 2\).
C
3. \(x = 1\) và \(y = - 3\).
D
4. \(x = 2\) và \(y = 1\).

Question 17

Câu 17:

Cho \(a\) là số thực dương khác \(1\). Tính \(I = {\log _a}\sqrt[3]{a}\).

A
1. \(I = - 3\).
B
2. \(I = 0\).
C
3. \(I = 3\).
D
4. \(I = \frac{1}{3}\).

Question 18

Câu 18:

Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số sau: Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1

A
1. \(y = \frac{{x - 2}}{{x + 1}}\).
B
2. \(y = {x^4} - 2{x^2} - 2\).
C
3. \(y = {x^3} - 2{x^2} - 2\).
D
4. \(y = - {x^4} + 2{x^2} - 2\).

Question 19

Câu 19:

Trong không gian Oxyz, đường thẳng d: \(\left\{ \begin{gathered} x = 2 + 3t \hfill \\ y = – 1 – 4t \hfill \\ z = 5t \hfill \\ \end{gathered} \right.\) đi qua điểm nào sau đây?

A
1. \(M(5;\,5;\,5)\)
B
2. \(M(8;\,9;\,10)\)
C
3. \(M(3;\, - 4;\,5)\)
D
4. \(M(2;\, - 1;\,0)\)

Question 20

Câu 20:

Có bao nhiêu cách lấy hai con bài từ cỗ bài tú lơ khơ gồm \(52\) con?

A
1. \(450.\)
B
2. \(1326.\)
C
3. \(104.\)
D
4. \(2652.\)

Question 21

Câu 21:

Cho hình lăng trụ đứng có diện tích đáy là \(\sqrt 3 {a^2}\). Độ dài cạnh bên là \(a\sqrt 2 \). Khi đó thể tích của khối lăng trụ là:

A
1. \(\sqrt 3 {a^3}\).
B
2. \(\sqrt 6 {a^3}\).
C
3. \(\frac{{\sqrt 6 {a^3}}}{3}\).
D
4. \(\sqrt 2 {a^3}\).

Question 22

Câu 22:

Tìm đạo hàm của hàm số \(y = {\pi ^x}\).

A
1. \(y' = x{\pi ^{x - 1}}\).
B
2. \(y' = {\pi ^x}\ln \pi \).
C
3. \(y' = \frac{{{\pi ^x}}}{{\ln \pi }}\).
D
4. \(y' = x{\pi ^{x - 1}}\ln \pi \).

Question 23

Câu 23:

Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1 Khẳng định nào sau đây đúng?

A
1. Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).
B
2. Hàm số đồng biến trên khoảng \(\left( { - 1;1} \right).\)
C
3. Hàm số đồng biến trên khoảng \(\left( { - 1;3} \right)\).
D
4. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).

Question 24

Câu 24:

Cho khối trụ có chiều cao bằng \(4a\) và bán kính đáy bằng \(2a\). Thể tích khối trụ đã cho bằng

A
1. \(16\pi {a^3}\).
B
2. \(\frac{{32}}{3}\pi {a^3}\).
C
3. \(32\pi {a^3}\).
D
4. \(\frac{{16}}{3}\pi {a^3}\).

Question 25

Câu 25:

Cho \(\int\limits_2^5 {f\left( x \right){\text{d}}x} = 10\). Khi đó \(\int\limits_5^2 {\left[ {2 – 4f\left( x \right)} \right]{\text{d}}x} \) bằng :

A
1. \(36\) .
B
2. \(40\) .
C
3. \(34\) .
D
4. \(32\) .

Question 26

Câu 26:

Cho cấp số cộng \(\left( {{u_n}} \right)\) có \(\;{u_1} = 11\) và công sai \(d = 4\). Hãy tính \({u_{99}}\).

A
1. \(401.\)
B
2. \(403.\)
C
3. \(402.\)
D
4. \(404.\)

Question 27

Câu 27:

Phát biểu nào sau đây là phát biểu đúng?

A
1. \(\int {\sin 2xdx = \frac{{\cos 2x}}{2} + C,C \in \mathbb{R}} \).
B
2. \(\int {\sin 2xdx = \frac{{ - \cos 2x}}{2} + C,C \in \mathbb{R}} \)
C
3. \(\int {\sin 2xdx = \cos 2x + C,C \in \mathbb{R}} \).
D
4. \(\int {\sin 2xdx = 2\cos 2x + C,C \in \mathbb{R}} \).

Question 28

Câu 28:

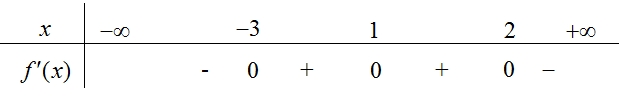Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) với bảng xét dấu đạo hàm như sau: Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1 Số điểm cực trị của hàm số \(y = f(x)\) là

A
1. \(3\).
B
2. \(0\).
C
3. \(1\).
D
4. \(2\).

Question 29

Câu 29:

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{{x^3}}}{3} + 2{x^2} + 3x – 4\) trên đoạn \(\left[ { – 4;\,0} \right]\) lần lượt là \(M\) và \(n\). Giá trị của tổng \(M + n\) bằng

A
1. \( - \frac{{28}}{3}\).
B
2. \( - 4\).
C
3. \( - \frac{4}{3}\).
D
4. \(\frac{4}{3}\).

Question 30

Câu 30:

Hàm số nào dưới đây đồng biến trên \(\mathbb{R}\)?

A
1. \(y = \frac{1}{3}{x^3} - \frac{1}{2}{x^2} + 3x + 1\).
B
2. \(y = {x^3} + 4{x^2} + 3x - 1\) .
C
3. \(y = {x^4} - 2{x^2} - 1\).
D
4. \(y = \frac{{x - 1}}{{x + 2}}\).

Question 31

Câu 31:

Với \(a\), \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng

A
1. \(2\left( {\log a + \log b} \right)\).
B
2. \(\log a + 2\log b\).
C
3. \(2\log a + \log b\).
D
4. \(\log a + \frac{1}{2}\log b\).

Question 32

Câu 32:

Cho hình lập phương \(ABCD:)A'B'C'D'\), góc giữa hai đường thẳng \(A'B\) và \(B'C\) là

A
1. \(90^\circ \).
B
2. \(60^\circ \).
C
3. \(45^\circ \).
D
4. \(30^\circ \).

Question 33

Câu 33:

Cho \(\int\limits_1^2 {\left[ {4f\left( x \right) – 2x} \right]dx = 1.} \) Khi đó \(\int\limits_1^2 {f\left( x \right)dx} \) bằng :

A
1. \(1\).
B
2. \( - 3\).
C
3. \(3\).
D
4. \( - 1\).

Question 34

Câu 34:

Trong không gian với hệ toạ độ \(Oxyz\), cho đường thẳng \(\left( d \right):\frac{{x + 2}}{2} = \frac{y}{{ – 1}} = \frac{{z – 3}}{{ – 3}}\) và điểm \(B\left( { – 1;0;2} \right)\). Viết phương trình mặt phẳng \(\left( P \right)\) đi qua \(B\) và vuông góc đường thẳng \(\left( d \right)\).

A
1. \(2x + y + 3z - 4 = 0\).
B
2. \(2x + y - 3z + 8 = 0\).
C
3. \(2x - y + 3z - 4 = 0\).
D
4. \(2x - y - 3z + 8 = 0\).

Question 35

Câu 35:

Cho số phức \(z\) thỏa mãn \(\left( {1 + 2i} \right)z = 5{\left( {1 + i} \right)^2}\). Tổng bình phương phần thực và phần ảo của số phức \(w = \bar z + iz\) bằng:

A
1. \(2\).
B
2. \(4\).
C
3. \(6\).
D
4. \(8\).

Question 36

Câu 36:

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = a\),\(BC = a\sqrt 2 \), đường thẳng \(SA\) vuông góc với mặt phẳng đáy và góc giữa đường thẳng \(SC\) và mặt phẳng đáy bằng \({30^0}\). Gọi \(h\) là khoảng cách từ điểm \(S\) đến mặt phẳng \(\left( {ABC} \right)\). Mệnh đề nào dưới đây là đúng?

A
1. \(h = \frac{a}{2}\).
B
2. \(h = 3a\).
C
3. \(h = a\).
D
4. \(h = a\sqrt 3 \).

Question 37

Câu 37:

Gieo một con súc sắc. Xác suất để mặt chấm chẵn xuất hiện là:

A
1. \(0,3\).
B
2. \(0,4\).
C
3. \(0,5\).
D
4. \(0,2\).

Question 38

Câu 38:

Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(A\left( {2; – 1;3} \right)\) và mặt phẳng \(\left( P \right):2x – 3y + z – 1 = 0\). Viết phương trình đường thẳng \(d\) đi qua \(A\) và vuông góc với \(\left( P \right)\).

A
1. \(d:\frac{{x - 2}}{2} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 1}}{3}\)
B
2. \(d:\frac{{x + 2}}{2} = \frac{{y - 1}}{{ - 3}} = \frac{{z + 3}}{1}\)
C
3. \(d:\frac{{x - 2}}{2} = \frac{{y + 1}}{{ - 3}} = \frac{{z - 3}}{1}\)
D
4. \(d:\frac{{x - 2}}{2} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 3}}{3}\)

Question 39

Câu 39:

Tổng tất cả các nghiệm của phương trình \({4^x} – {8.2^x} + 4 = 0\) bằng bao nhiêu?

A
1. \(8\).
B
2. \(1\).
C
3. \(0\).
D
4. \(2\).

Question 40

Câu 40:

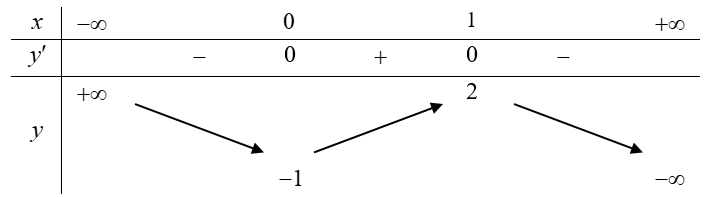Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1 Số nghiệm của phương trình \(f\left( {2 – x} \right) – 1 = 0\) là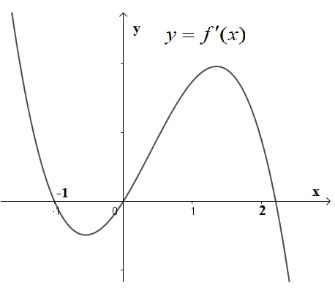

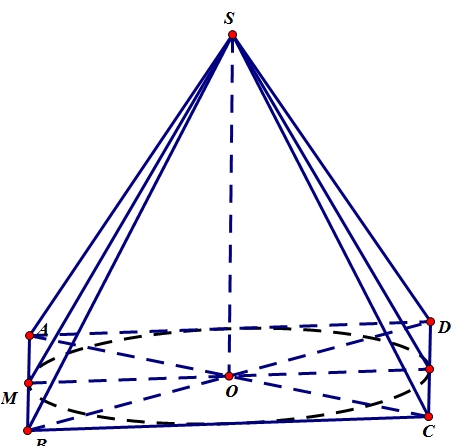A
1. \(3\).
B
2. \(2\).
C
3. \(1\).
D
4. \(0\).

Question 41

Câu 41:

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Biết \(\int\limits_1^{{e^3}} {\frac{{f\left( {\operatorname{lnx} } \right)}}{x}} dx = 7\), \(\int\limits_0^{\frac{\pi }{2}} {f\left( {\cos x} \right).\sin x} dx = 3\). Tính \(\int\limits_1^3 {\left( {f\left( x \right) + 2x} \right)} dx\).

A
1. \(12\).
B
2. \(15\).
C
3. \( - 10\).
D
4. \(10\).

Xét tích phân \(A = \int\limits_1^{{e^3}} {\frac{{f\left( {\ln x} \right)}}{x}} dx\).Đặt \(t = \ln x \Rightarrow dt = \frac{1}{x}dx\), đổi cận \(x = 1 \Rightarrow t = 0\), \(x = {e^3} \Rightarrow t = 3\).Do đó \(A = \int\limits_0^3 {f\left( t \right)dt} = \int\limits_0^3 {f\left( x \right)dx} \).Xét tích phân \(B = \int\limits_0^{\frac{\pi }{2}} {f\left( {\cos x} \right).\sin x} dx\).Đặt \(u = \cos x \Rightarrow du = – \sin xdx\), đổi cận \(x = 0 \Rightarrow u = 1\), \(x = \frac{\pi }{2} \Rightarrow u = 0\).Do đó \(A = \int\limits_1^0 { – f\left( u \right)du} = \int\limits_0^1 {f\left( x \right)dx} \).Xét \(\int\limits_1^3 {\left( {f\left( x \right) + 2x} \right)} dx\)\( = \int\limits_1^3 {f\left( x \right)} dx + \int\limits_1^3 {2x} dx = \)\(\int\limits_0^3 {f\left( x \right)} dx – \int\limits_0^1 {f\left( x \right)} dx + \left. {{x^2}} \right|_1^3\)\( = 7 – 3 + 8 = 12\).

Question 42

Câu 42:

Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Hình chiếu của \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) trùng với trung điểm của cạnh \(AB\). Cạnh bên \(SD = \frac{{3a}}{2}\). Tính thể tích khối chóp \(S.ABCD\) theo \(a\).

A
1. \(\frac{{\sqrt 2 }}{3}{a^3}\).
B
2. \(\frac{{\sqrt 3 }}{3}{a^3}\).
C
3. \(\frac{{\sqrt 5 }}{3}{a^3}\).
D
4. \(\frac{1}{3}{a^3}\).

Gọi \(H\) là trung điểm của \(AB\) thì \(SH \bot \left( {ABCD} \right)\). Ta có \(HD = \frac{{a\sqrt 5 }}{2}\) nên \(SH = \sqrt {\frac{{9{a^2}}}{4} – \frac{{5{a^2}}}{4}} = a\).\({V_{S.ABCD}} = \frac{1}{3}SH.{S_{ABCD}}\)\( = \frac{1}{3}.a.{a^2} = \frac{{{a^3}}}{3}\).

Question 43

Câu 43:

Gọi \({z_1},{z_2}\) là hai nghiệm phức của phương trình \({z^2} – z + 1 = 0\). Giá trị của \(\left| {{z_1}} \right| + \left| {{z_2}} \right|\) bằng.

A
1. \(4\).
B
2. \(1\).
C
3. \(2\).
D
4. \(0\).

\({z^2} – z + 1 = 0\)\( \Leftrightarrow {z_1} = \frac{1}{2} + \frac{{\sqrt 3 }}{2}i \vee {z_2} = \frac{1}{2} – \frac{{\sqrt 3 }}{2}i\)Khi đó: \(\left| {{z_1}} \right| + \left| {{z_2}} \right| = 2\sqrt {\frac{1}{4} + \frac{3}{4}} = 2\).

Question 44

Câu 44:

Cho số phức \(z\) thỏa mãn \(5\left| {z – i} \right| = \left| {z + 1 – 3i} \right| + 3\left| {z – 1 + i} \right|\). Tìm giá trị lớn nhất \(M\) của \(\left| {z – 2 + 3i} \right|\) ?

A
1. \(M = 4\sqrt 5 \)
B
2. \(M = 1 + \sqrt {13} \)
C
3. \(M = 9\)
D
4. \(M = \frac{{10}}{3}\)

Gọi \(A\left( {0;1} \right)\), \(B\left( { – 1;3} \right),C\left( {1; – 1} \right)\). Ta thấy \(A\) là trung điểm của \(BC\)\( \Rightarrow M{A^2} = \frac{{M{B^2} + M{C^2}}}{2} – \frac{{B{C^2}}}{4}\) \( \Leftrightarrow M{B^2} + M{C^2} = 2M{A^2} + \frac{{B{C^2}}}{2} = 2M{A^2} + 10\).Ta lại có : \(5\left| {z – i} \right| = \left| {z + 1 – 3i} \right| + 3\left| {z – 1 + i} \right|\)\( \Leftrightarrow 5MA = MB + 3MC \leqslant \sqrt {10} .\sqrt {M{B^2} + M{C^2}} \)\( \Rightarrow 25M{A^2} \leqslant 10\left( {2M{A^2} + 10} \right)\) \( \Rightarrow MC \leqslant 2\sqrt 5 \)Mà \(\left| {z – 2 + 3i} \right| = \left| {\left( {z – i} \right) + \left( { – 2 + 4i} \right)} \right|\)\( \leqslant \left| {z – i} \right| + \left| {2 – 4i} \right|\)\( \leqslant \left| {z – i} \right| + 2\sqrt 5 \leqslant 4\sqrt 5 \).Dấu xảy ra khi \(\left\{ \begin{gathered} \left| {z – i} \right| = 2\sqrt 5 \hfill \\ \frac{a}{{ – 2}} = \frac{{b – 1}}{4} \hfill \\ \end{gathered} \right.\), với \(z = a + bi\); \(a,{\text{ }}b \in \mathbb{R}\).\( \Leftrightarrow \left[ \begin{gathered} z = 2 – 3i{\text{ }}\left( {loai} \right) \hfill \\ z = – 2 + 5i \hfill \\ \end{gathered} \right.\).

Question 45

Câu 45:

Cho hàm số \(f(x) = a{x^4} + b{x^3} + c{x^2} + dx + e\). Hàm số \(y = f'(x)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng? Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1

A
1. \(a + c < b + d\).
B
2. \(a + b + c + d < 0\).
C
3. \(b + d - c > 0\).
D
4. \(a + c > 0\).

Question 46

Câu 46:

Trong không gian với hệ tọa độ \(Oxyz\), cho \(A\left( {1; – 4;0} \right)\),\(B\left( {3;0;0} \right)\). Viết phương trình đường trung trực \(\left( \Delta \right)\) của đoạn \(AB\) biết \(\left( \Delta \right)\) nằm trong mặt phẳng \(\left( \alpha \right):x + y + z = 0\).

A
1. \(\Delta :\left\{ \begin{gathered} x = 2 + 2t \hfill \\ y = - 2 - t \hfill \\ z = 0 \hfill \\ \end{gathered} \right.\).
B
2. \(\Delta :\left\{ \begin{gathered} x = 2 + 2t \hfill \\ y = 2 - t \hfill \\ z = - t \hfill \\ \end{gathered} \right.\).
C
3. \(\Delta :\left\{ \begin{gathered} x = 2 + 2t \hfill \\ y = - 2 - t \hfill \\ z = - t \hfill \\ \end{gathered} \right.\).
D
4. \(\Delta :\left\{ \begin{gathered} x = 2 + 2t \hfill \\ y = - 2 - t \hfill \\ z = t \hfill \\ \end{gathered} \right.\).

\(\left( \alpha \right)\) có VTPT \(\vec n = \left( {1;1;1} \right)\), \(\overrightarrow {AB} = \left( {2;4;0} \right)\)\( \Rightarrow \left[ {\vec n;\overrightarrow {AB} } \right] = \left( { – 4;2;2} \right)\).\(\left( \Delta \right)\) có VTCP \(\vec u = \left( {2; – 1; – 1} \right)\).Gọi \(I\) là trung điểm của \(AB\). Khi đó \(I\left( {2; – 2;0} \right)\).PT \(\left( \Delta \right):\left\{ \begin{gathered} x = 2 + 2t \hfill \\ y = – 2 – t \hfill \\ z = – t \hfill \\ \end{gathered} \right.\).\(A\left( {3;\;3;\;1} \right)\).

Question 47

Câu 47:

Cho hình chóp tứ giác đều \(S.ABCD\) có các cạnh đều bằng \(a\sqrt 2 \). Tính thể tích khối nón có đỉnh \(S\) và đường tròn đáy là đường tròn nội tiếp tứ giác \(ABCD\).

A
1. \(V = \frac{{\sqrt 2 \pi {a^3}}}{2}\).
B
2. \(V = \frac{{\pi {a^3}}}{6}\).
C
3. \(V = \frac{{\sqrt 2 \pi {a^2}}}{6}\).
D
4. \(V = \frac{{\pi {a^3}}}{2}\).

Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1

Gọi \(O\) là tâm của hình bình hành \(ABCD\) \( \Rightarrow SO \bot \left( {ABCD} \right)\).Ta có : \(OA = \frac{1}{2}AC\) \( = a\) \( \Rightarrow SO = \sqrt {S{A^2} – A{O^2}} \) \( = a\).Hình nón đỉnh \(S\) có chiều cao \(h = SO\) \( = a\), bán kính đáy \(r = \frac{{a\sqrt 2 }}{2}\), có thể tích là :\(V = \frac{1}{3}{\text{\pi }}{r^2}h\) \( = \frac{{{\text{\pi }}{a^3}}}{6}\).

Question 48

Câu 48:

Gọi \(S\) là tổng tất cả các giá trị nguyên của \(m\) để bất phương trình \(\ln \left( {7{x^2} + 7} \right) \geqslant \ln \left( {m{x^2} + 4x + m} \right)\) nghiệm đúng với mọi \(x\) thuộc \(\mathbb{R}\). Tính \(S\).

A
1. \(S = 12\).
B
2. \(S = 35\).
C
3. \(S = 0\).
D
4. \(S = 14\).

Ta có: \(\ln \left( {7{x^2} + 7} \right) \geqslant \ln \left( {m{x^2} + 4x + m} \right)\)\( \Leftrightarrow \left\{ \begin{gathered} 7{x^2} + 7 \geqslant m{x^2} + 4x + m \hfill \\ m{x^2} + 4x + m > 0 \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {\left( {7 – m} \right){x^2} – 4x + 7 – m \geqslant 0\;\;\left( 1 \right)} \\ {m{x^2} + 4x + m > 0\;\;\left( 2 \right)} \end{array}} \right.\)Bất phương trình đã cho đúng với mọi \(x \in \mathbb{R}\) khi và chỉ khi các bất phương trình \(\left( 1 \right),\left( 2 \right)\) đúng với mọi \(x \in \mathbb{R}\).Xét \(\left( {7 – m} \right){x^2} – 4x + 7 – m \geqslant 0\) \(\left( 1 \right)\).+ Khi \(m = 7\) ta có \(\left( 1 \right)\) trở thành \( – 4x \geqslant 0 \Leftrightarrow x \leqslant 0\). Do đó \(m = 7\) không thỏa mãn.+ Khi \(m \ne 7\) ta có \(\left( 1 \right)\) đúng với mọi \(x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{gathered} 7 – m > 0 \hfill \\ \Delta ' \leqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m < 7 \hfill \\ 4 - {\left( {7 - m} \right)^2} \leqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m < 7 \hfill \\ m \leqslant 5 \vee m \geqslant 9 \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow m \leqslant 5\) \(\left( * \right)\).Xét \(m{x^2} - 4x + m > 0\) \(\left( 2 \right)\).+ Khi \(m = 0\) ta có \(\left( 2 \right)\) trở thành \( – 4x > 0 \Leftrightarrow x < 0\). Do đó \(m = 0\) không thỏa mãn.+ Khi \(m \ne 0\) ta có \(\left( 2 \right)\) đúng với mọi \(x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{gathered} m > 0 \hfill \\ \Delta ' < 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m > 0 \hfill \\ 4 – {m^2} < 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m > 0 \hfill \\ m < - 2 \vee m > 2 \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow m > 2\) \(\left( { * * } \right)\).Từ \(\left( * \right)\) và \(\left( { * * } \right)\) ta có \(2 < m \leqslant 5\). Do \(m \in Z\) nên \(m \in \left\{ {3;4;5} \right\}\). Từ đó \(S = 3 + 4 + 5 = 12\).

Question 49

Câu 49:

Trong không gian \(Oxyz\), cho tứ diện \(ABCD\) với \(A\left( {m;0;0} \right)\), \(B\left( {0;m – 1;0} \right)\); \(C\left( {0;0;m + 4} \right)\) thỏa mãn \(BC = AD\), \(CA = BD\) và \(AB = CD\). Giá trị nhỏ nhất của bán kính mặt cầu ngoai tiếp tứ diện \(ABCD\) bằng

A
1. \(\sqrt {14} \).
B
2. \(\sqrt 7 \).
C
3. \(\frac{{\sqrt {14} }}{2}\).
D
4. \(\frac{{\sqrt 7 }}{2}\) .

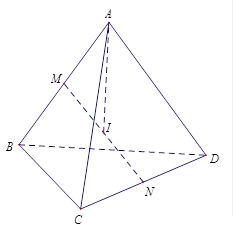Đặt \(BC = a\); \(CA = b\); \(AB = c\) .Gọi \(M\), \(N\) lần lượt là trrung điểm của \(AB\) và \(CD\).Theo giả thiết ta có tam giác \(\Delta ABC = \Delta CDA\) \(\left( {c.c.c} \right)\)\( \Rightarrow CM = DM\) hay tam giác \(CMD\) cân tại \(M\) \( \Rightarrow MN \bot CD\).Chứng minh tương tự ta cũng có \(MN \bot AB\).Gọi \(I\) là trung điểm của \(MN\) thì \(IA = IB\) và \(IC = ID\).Mặt khác ta lại có \(AB = CD\) nên \(\Delta BMI = \Delta CNI\) \( \Rightarrow IB = IC\) hay \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\).Ta có \(I{A^2} = I{M^2} + A{M^2}\)\( = \frac{{M{N^2}}}{4} + \frac{{A{B^2}}}{4}\)\( = \frac{{M{N^2} + {c^2}}}{4}\).Mặt khác \(CM\) là đường trung tuyến của tam giác \(ABC\) nên \(C{M^2} = \frac{{2{a^2} + 2{b^2} – {c^2}}}{4}\) \( \Rightarrow M{N^2} = C{I^2} – C{N^2}\)\( = \frac{{2{a^2} + 2{b^2} – {c^2}}}{4} – \frac{{{c^2}}}{4}\)\( = \frac{{{a^2} + {b^2} – {c^2}}}{2}\).Vậy \(I{A^2} = \frac{{{a^2} + {b^2} + {c^2}}}{8}\).Với \({a^2} + {b^2} + {c^2} = 2{m^2} + 2{\left( {m – 1} \right)^2} + 2{\left( {m + 4} \right)^2}\)\( = 6{\left( {m + 1} \right)^2} + 28\)Vậy \(I{A^2} = \frac{{6{{\left( {m + 1} \right)}^2} + 28}}{8} \geqslant \frac{7}{2}\)\( \Rightarrow I{A_{\min }} = \sqrt {\frac{7}{2}} = \frac{{\sqrt {14} }}{2}\).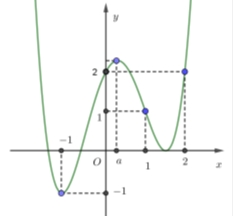

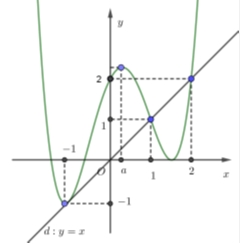Question 50

Câu 50:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) cho bởi hình vẽ bên. Đặt \(g\left( x \right) = f\left( x \right) – \frac{{{x^2}}}{2}\), \(\forall x \in \mathbb{R}\). Hỏi đồ thị hàm số \(y = g\left( x \right)\) có bao nhiêu điểm cực trị ? Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1

A
1. \(4\).
B
2. \(1\).
C
3. \(2\).
D
4. \(3\).

\(g'\left( x \right) = f'\left( x \right) – x\) Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1

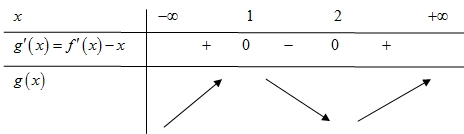Từ đồ thị hàm số \(y = f'\left( x \right)\) và đồ thị hàm số \(y = x\) ta thấy \(f'\left( x \right) – x > 0\) với \(\forall x \in \left( { – \infty ;1} \right) \cup \left( {2; + \infty } \right)\)\(f'\left( x \right) – x < 0\) với \(\forall x \in \left( {1;2} \right)\)Ta có bảng biến thiên của \(g\left( x \right)\) Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1

Vậy đồ thị hàm số \(y = g\left( x \right)\) có hai điểm cực trị.

Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1

Đề Kiểm Tra: Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1

Các lựa chọn đã được chọn:

Đáp án: Đề Thi Thử Tốt Nghiệp THPT 2023 Môn Toán Online-Đề 1

Trắc Nghiệm Liên Quan

Đề Thi Thử Tốt Nghiệp 2022 Môn Toán Online Bám Sát Đề Tham Khảo(Đề 4)

Đề Thi Thử TN 2022 Online Môn Toán Theo Đề Minh Họa-Đề 3

Đề Thi Thử Tốt Nghiệp 2022 Online Môn Toán Bám Sát Đề Tham Khảo-Đề 2

Đề Thi Thử Tốt Nghiệp THPT 2022 Online Môn Toán Bám Sát Đề Tham Khảo-Đề 1

Kiểm Tra 15 Phút Online Bài Mệnh Đề Toán 10 (Đề 1)

Đề Thi Thử Tốt Nghiệp THPT Năm 2023 Môn Toán Online-Đề 2

Đề Thi Thử Tốt Nghiệp THPT 2023 Online Môn Toán-Đề 3

Kiểm Tra 15 Phút Online Bài Mệnh Đề Lớp 10 (Đề 2)

Kiểm Tra 15 Phút Online Bài Tập Hợp Và Các Phép Toán Trên Tập Hợp-Đề 1

Kiểm Tra 15 Phút Trực Tuyến Bài Tập Hợp Và Các Phép Toán Trên Tập Hợp-Đề 2

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN