
Danh Mục Sách
- Thiếu nhi
- Giáo khoa - Tham khảo
- Văn học
- Tâm lý - Kỹ năng sống
- Manga - Comic
- Sách học ngoại ngữ
- Kinh Tế
- Khoa học kỹ thuật
- Lịch Sử - Địa Lý - Tôn Giáo
- Nuôi Dạy Con
- Chính Trị - Pháp Lý - Triết Học
- Tiểu Sử Hồi Ký
- Đam Mỹ
- Nữ Công Gia Chánh
- Văn Hóa - Nghệ Thuật - Du Lịch
- Phong Thủy - Kinh Dịch
- Từ điển
- Âm Nhạc - Mỹ Thuật - Thời Trang
- Thể Dục Thể thao - Giải Trí
- Báo - Tạp Chí
- Giáo trình
- Làm Vườn - Thú Nuôi
- Mystery Box
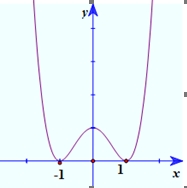 Chọn đáp án sai.
Chọn đáp án sai.