Từ đồ thị hàm số \(f'\left( x \right)\) ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered} x = {x_1} \hfill \\ x = 1 \hfill \\ x = {x_2} \hfill \\ \end{gathered} \right.\) với \( – 1 < {x_1} < 1 < {x_2} < 2\).Từ đó suy ra bảng biến thiên của hàm số\(f\left( x \right)\) là:
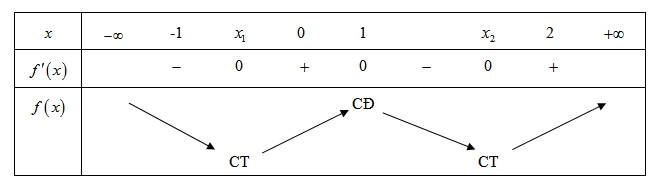
Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { – \infty \,;\,{x_1}\,} \right)\), \( – 3 < - 2 < {x_1}\) \( \Rightarrow f\left( { - 3} \right) > f\left( { – 2} \right)\). Nên A sai.Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { – \infty \,;\,{x_1}\,} \right)\) , \(\left( { – \infty \,;\, – 1} \right) \subset \left( { – \infty \,;\,{x_1}\,} \right)\)\( \Rightarrow \)hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( { – \infty \,;\, – 1} \right)\). Nên B sai.Qua \(x = 0\) đạo hàm \(f'\left( x \right)\) không đổi dấu nên \(x = 0\) không là điểm cực trị. Nên D sai.Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {\,{x_1}\,\,;\,1\,} \right)\), \({x_1} < 0 < 1\) \( \Rightarrow f\left( 0 \right) < f\left( 1 \right)\).

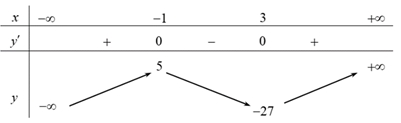
 Tìm khoảng đồng biến của hàm số đã cho.
Tìm khoảng đồng biến của hàm số đã cho.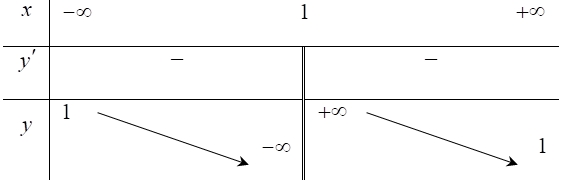
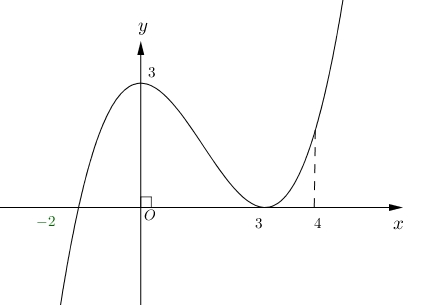
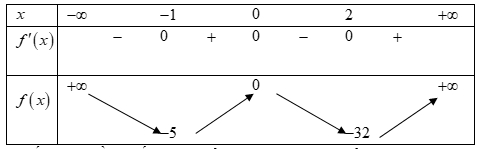 Hỏi hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
Hỏi hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?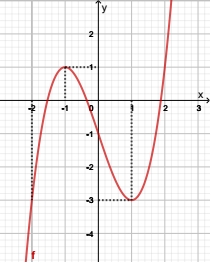 Hàm số đồng biến trên khoảng nào dưới đây?
Hàm số đồng biến trên khoảng nào dưới đây?
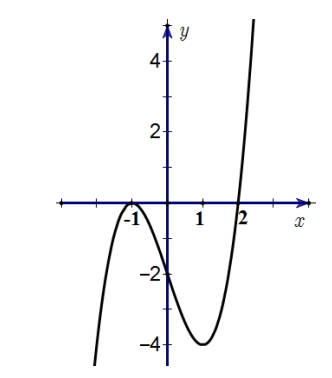 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?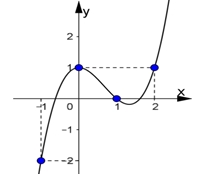
 Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { – \infty \,;\,{x_1}\,} \right)\), \( – 3 < - 2 < {x_1}\) \( \Rightarrow f\left( { - 3} \right) > f\left( { – 2} \right)\). Nên A sai.Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { – \infty \,;\,{x_1}\,} \right)\) , \(\left( { – \infty \,;\, – 1} \right) \subset \left( { – \infty \,;\,{x_1}\,} \right)\)\( \Rightarrow \)hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( { – \infty \,;\, – 1} \right)\). Nên B sai.Qua \(x = 0\) đạo hàm \(f'\left( x \right)\) không đổi dấu nên \(x = 0\) không là điểm cực trị. Nên D sai.Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {\,{x_1}\,\,;\,1\,} \right)\), \({x_1} < 0 < 1\) \( \Rightarrow f\left( 0 \right) < f\left( 1 \right)\).
Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { – \infty \,;\,{x_1}\,} \right)\), \( – 3 < - 2 < {x_1}\) \( \Rightarrow f\left( { - 3} \right) > f\left( { – 2} \right)\). Nên A sai.Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { – \infty \,;\,{x_1}\,} \right)\) , \(\left( { – \infty \,;\, – 1} \right) \subset \left( { – \infty \,;\,{x_1}\,} \right)\)\( \Rightarrow \)hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( { – \infty \,;\, – 1} \right)\). Nên B sai.Qua \(x = 0\) đạo hàm \(f'\left( x \right)\) không đổi dấu nên \(x = 0\) không là điểm cực trị. Nên D sai.Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {\,{x_1}\,\,;\,1\,} \right)\), \({x_1} < 0 < 1\) \( \Rightarrow f\left( 0 \right) < f\left( 1 \right)\).